FizykaII51401

510

użyć teorycznycli, na rachunku opartych poszukiwań, które bez trudności można elementarnie przeprowadzić, jak następuje:

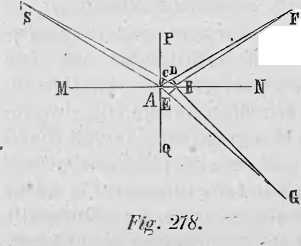
Przy odbiciu i załamanie się promienia BA {Fig. 278) ruch cząsteczek eteru w przestrzeni ABC przenosi się na cząsteczki eteru, zawartego w przestrzeniach ABD i ABE. Lecz przestrzeń ABD - ABC, a przestrzeń ABE: ABC.—AE. BE : AC. BC. Oznaczywszy więc kąt padania &•//•'przez «, kąt załamania QAG przez //, mamy też CiB — a, AEB—@, zatem AC=AB cos «, BC— AB sin a, AE — AB sin (3, BE J AB cos /?, a owa proporeya przechodzi w następującą: zfZ?C: ABE = ąpt « u : «tn co-s p’.

Jeżeli gęstości eteru w obydwóch graniczących ze sobą pośrednikach światła mają się do siebie jak d : d\ masy jego, zawarte w przestrzeniach ABC i ABE, są do siebie w stosunku d sin a cos a : d' sin (3 cos {3.

W przypuszczeniu, że ruch drgający udziela się według praw uderzenia ciał elastycznych, zatem prawo zachowania żywej siły ruchu ma tu swoje zastosowanie, a natężenie drgania w promieniu padającym jest c, w odbitym x, w załamanym y, możemy ułożyć zrównanie

d sin ff cos a c³ — d sin a cos cc. x² -j- d' sin § cos j3. y³

czyli

1) (c^s — x²) d sin u cos « — i/³, cl' sin 6 cos 3. Przyjąwszy.dalej, że przesyłanie poprzecznych drgań w eterze odbywa się podobnie, jak wzdłuż napiętej struny, a prężność eteru w obu pośrednikach światła jest równa, (co do utrzymania jego stanu równowagi jest koniecznem), chyżości przesyłania fal światła w tych pośredni kaci) mieć się będą do siebie odwrotnie, jak kwadratowe pierwiastki z ich gęstości (§ 7). Lecz chyżości te mają się też do siebie (§ 74) jak sin a : sin (3, dla tego mamy proporcyą

1 1 sM ^: ~jd' ’

sin ci : sin {3 Ę=:

czyli d\d' = sin 6³: sin a²,