zad08

Data

ĆWICZENIA 8.

Ruch obrotowy bryły sztywnej.

Moment siły:    M = r x F

I    zasada dynamiki ruchu obrotowego:

Jeżeli na bryłą działają siły, których suma momentów względem osi obrotu jest równa zeru, to ciało pozostaje w spoczynku lub obraca się ruchem obrotowym jednostajnym.

II    zasada dynamiki ruchu obrotowego:

Jeżeli na bryłę sztywną działa stały moment siły, to bryła obraca się ruchem przyspieszonym, w którym przyspieszenie kątowe s jest wprost proporcjonalne do przyłożonego momentu siły M

h/f    ⁿ

£ = —, gdzie / jest momentem bezwładności ciała:    / = ^ m_i ■ r²

I    i=i

Energia kinetyczna ruchu obrotowego:

E_k = ^ ^    (to - prędkość kątowa)

Twierdzenie Steinera:

Moment bezwładności I względem dowolnej osi, równoległej do osi przechodzącej przez środek masy wyznaczamy ze wzoru:    I = I₀ + m -d², gdzie I₀ jest momentem bezwładności

względem osi przechodzącej przez środek masy, zaś d jest odległością między osiami.

Moment pędu (jest wektorem skierowanym wzdłuż osi obrotu zgodnie z regułą śruby prawoskrętnej): L = I G)

Zasada zachowania momentu pędu:

Jeżeli na bryłę sztywną nie działa żaden moment siły lub momenty działających sił równoważą się, to moment pędu bryły pozostaje stały.

Zad. ł Na nieważkim pręcie o długości L=2r umieszczono kulki o niewielkich rozmiarach i masach mi=lkg, m₂=2mi i m₃=3mi. Jakie będą momenty bezwładności względem osi Oj, 0₂, 0₃?

! Oi    I0₂    !0₃

6-

mi

m-

-Ó

m₃

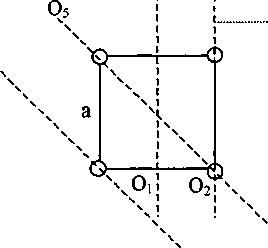
Zad.2 Oblicz moment bezwładności układu czterech kul, każda o masie m, znajdujących się w wierzchołkach kwadratu o boku a, względem osi obrotu Oi, 0₂, 0_3> O4, 0₅.    ₍

Zad.3 Tancerka wykonując piruet zbliża ramiona do tułowia. Czy, a jeśli tak to jak, zmieni się jej energia kinetyczna?

Zad.4 Jak zmieni się energia kinetyczna układu, jeśli zwiększymy dwukrotnie odległość mas od osi obrotu i równocześnie zwiększymy dwa razy prędkość kątową?

2co

Zad.5 Oblicz siłę tarcia T klocka hamulcowego, który w czasie t zahamował koło o momencie bezwładności I, promieniu r, obracające się z prędkością kątową co.

Zad.6 Walec o masie m, promieniu r (1=1/2 mr²) stacza się bez poślizgu z równi pochyłej o wysokości h. Jaką prędkość liniową osiągnie ten walec u podstawy równi?