1050

6.3. Zadania miarowe

Zmiana układu odniesienia (transformacja), obrót oraz kład posłużą do rozwiązywania kolejnych problemów miarowych.

6.3.1. Wielkość kąta między dwiema płaszczyznami

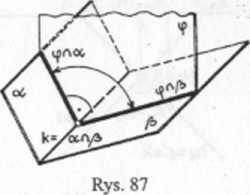
Kąt między dwiema płaszczyznami a i P jest kątem płaskim, leżącym w płaszczyźnie <p, prostopadłej do obu płaszczyzn, prostopadłej do ich wspólnej krawędzi (rys. 87 - poglądowy).

Przykład 6.2

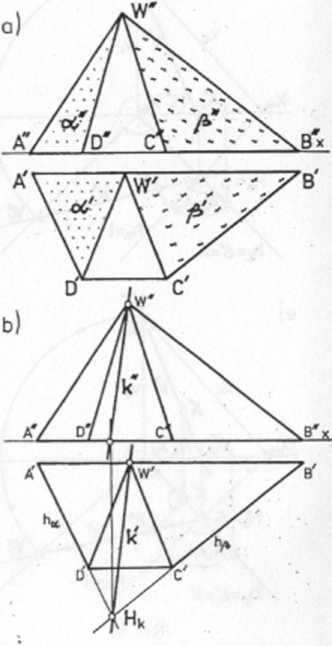
a)    W układzie dany jest ostrosłup o wierzchołkach A, B, C, D, W. Wierzchołki AWD wyznaczają płaszczyznę dowolną a, natomiast wierzchołki CWB płaszczyznę dowolną fi.

Znaleźć wartość kąta między płaszczyznami a i P wyznaczonymi przez ściany ostrosłupa.

b)    Wyznaczmy krawędź obu płaszczyzn a i p, tj. kikf, k").

Krawędź k wyznaczają dwa punkty wspólne:

-    wierzchołek WiJY', W")

-    punkt przecięcia się śladów poziomych obu płaszczyzn

Rzuty poziome i pionowe tych punktów wyznaczają rzuty k' i fc" krawędzi k (rys. 88b).

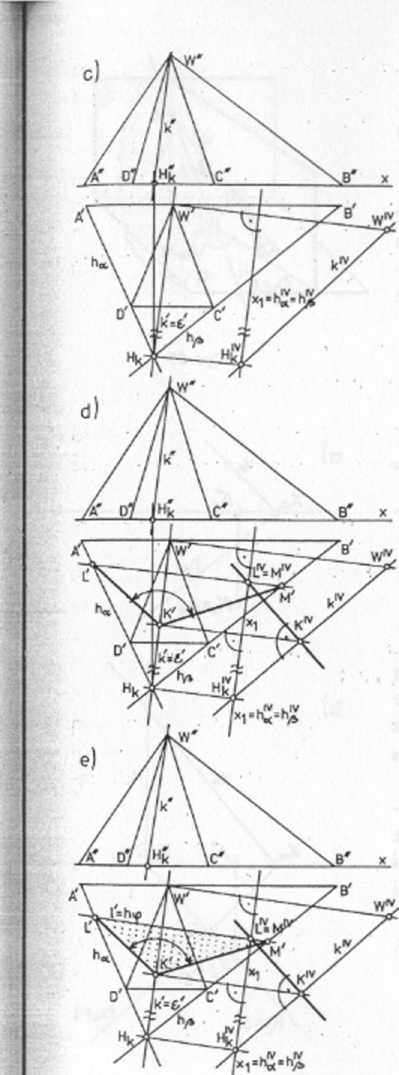
c)    Płaszczyznę kąta (p, prostopadłą do krawędzi k, najłatwiej wyznaczymy w rzucie na płaszczyznę rzutni dodatkowej, usytuowanej równolegle do krawędzi k_t tzn.

<-*,11

W tym celu skonstruujemy rzut na płaszczyznę n_A krawędzi k(W, H_k) (p. 4.3) oraz śladów poziomych płaszczyzn a i fi, tzn. h_a i (rys. 88c).

d)    Płaszczyzna kąta <pjest rzutująca na n_A (k || n_A, (p 1 k -> <p±7r₄), a jej rzut (fł^y jest prostopadły do rzutu A^^v w dowolnym punkcie.

Po wykonaniu w rzucie n_A przekroju płaszczyzną (p krawędzi k oraz śladów h i hp otrzymamy punkty:

/C^IV - przekrój krawędzi k,

L^w - przekrój śladu h_a,

M^iy - przekrój śladu hp

Po znalezieniu rzutów poziomych tych punktów, otrzymamy rzut kąta (rys. 88d)

ę= ZL'K'Af.

e)    Ponieważ płaszczyzna kąta (p nic jest równoległa do rzutni tt, nic można więc ocenić prawdziwej wielkości kąta.

Dokonując kładu płaszczyzny (p na 7T, otrzymamy rzeczywistą wielkość kąta (p.

Oś obrotu w tym kładzie jest wspólną częścią rzutni n, i płaszczyzny kąta (p, wyznaczoną przez punkty V i AT. Punkty te nie zmienią swojego położenia w kładzie. Punkt K natomiast

101