1145

Tablica 8.9. Obroty (w min zt) w badanym przedsiębiorstwie w latach 2000-2003

Lata	Kwartały	Obroty (min zł) K
2000	I	5.3
	II	12,7
	III	18,0
	IV	9,9
• 2001	I	7,5
	II	16.1
	III	23.2
	IV	13,2
2002	1	12,6
	II	15,9
	III	19,5
	IV	12
2003	1	11.9
	II	18,2
	III	22,3
	IV	18,9

Źródło: dane umowne.

Rysunek 8.4. Obroty w badanym przedsiębiorstwie w latach 2000-2003 (diagram czasowy)

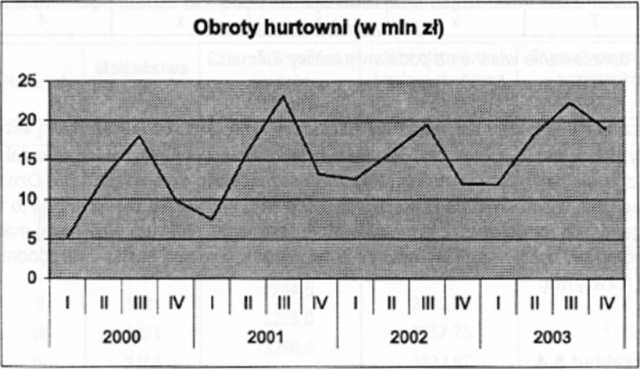
Źródło: opracowanie własne na podstawie danych z tablicy 8.9.

Na powyższym diagramie możemy obserwować, iż badane zjawisko w niektórych kwartałach rośnie, a w innych maleje. Najsilniejszy wzrost obserwowany jest w trzecim kwartale. Na tej podstawie możemy twierdzić, iż obroty w badanym przedsiębiorstwie z branży budowlanej uzależnione są od czynnika sezonowego.

Metoda analityczna wyznaczania czynników sezonowych oparta jest na głównej tendencji rozwojowej. Pierwszym krokiem w tej metodzie będzie wyznaczenie liniowej funkcji trendu postaci y_t = 6, - f + Z>₀, w analogiczny sposób jak to miało miejsce w przykładzie (8.1).

Korzystając z uzyskanych wyników powyższej tablicy wyznaczamy parametr bj i b₀: 136-237,2

2203,7-

16

2203,7-2016,2    187,5

1496-

(136)^ł

1496-1156

340

= 0.55,

16

Tablica 8.10 Obliczenia dla potrzeb wyznaczenia funkcji trendu

/		fy,	/^2
1	5.3	5.3	1
2	12.7	15.4	2
3	18.0	54,0	9
4	9.9	39.6	16
5	7.5	37.5	25
6	16.1	96,6	36
7	23,2	162.4	49
8	13,2	105.6	64
9	12.6	113,4	81
10	15.9	159.0	100
11	19,5	214.5	121
12	12.0	144.0	144
13	11.9	154,7	169
14	18.2	254.8	196
15	22,3	334.5	225
16	18.9	302,4	256
1=136	1=237,2	1=2203.7	1=1496

Źródło: opracowanie własne na podstawie tablicy 8.9.

-    ²³⁷*²    m₈*<    • 7    ¹³⁶    ₈ <

y =-= 14,825 i t =-= 8,5,

16 16

b₀ = 14,825 - 0,55 • 8,5 = 14,825 - 4,675 = 10,15.

Zatem linia trendu obrotów w badanym przedsiębiorstwie ma następującą postać:

y, =0,55/ +10,15.

Przystępujemy do wyznaczania czynników (wskaźników) sezonowych korzystając z modelu multiplikatywnego: Y_t=T, S, • I, (por wzór 8.8).

229