test6f4

edu q pjwstk

MENU

| Kurs +/ Oceny Materiały Bi Foldery zadań Chat

Bj))) Ogłoszenia & Testy 2 ⁼ Inny kurs ^ Wyloguj

Administrator

TESTY2    Załogowany: Arkadiusz Bochenek Kurs: Algorytmy i struktury danych (ASP) - studia dzienne    POMOC    WYLOGUJ

Twój wynik: 1 punktów na 6 możliwych do uzyskania (16,67 %).

Bochenek Arkadiusz

Opcja |

Punkty

Poprawna |

| Odpowiedź

Rozważmy algorytm HeapDestroy postaci:

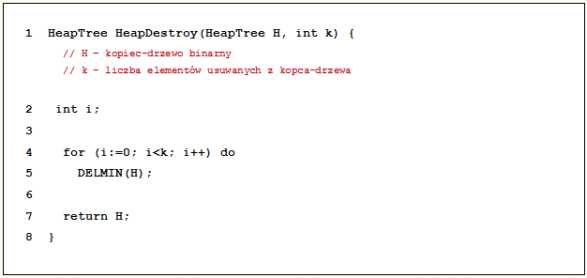
Niech kopiec H będzie rezultatem działania algorytmu HeapDestroy dla danych wejściowych:

•    kopiec-drzewo początkowy ^H = HeopSiowCon.słrticf([6,9,15,0,18,ll,13,2,16,3]) _ _gdzie ajgo^ HeapSlowConstract jest wolnym algotytmem budowy kopca-drzew^ra (przez kolejne wstawianie elementów),

•    liczba usmyanych elementów k = 5.

Które z poniższych zdań jest praw'dziw^re?

Etykiety wierzchołków' kopca-drzew^ra H wypisane w kolejności PreOrder tworzą ciąg: 11,13,16,13,15	i	+
Etykiety wierzchołków' kopca-drzew^ra H wypisane w kolejności PostOrder tworzą ciąg: 16,13,13,15,11	i	+
Liczba wierzchołków wewnętrznych kopca-drzew^ra H jest równa dokładnie 1	0

Rozważmy algorytm HeapDestroy postaci:

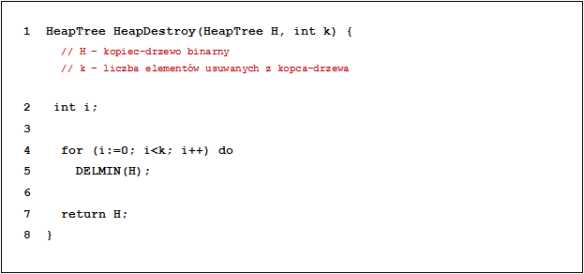
Które z poniższych zdań jest prawdziwe, jeżeli n jest początkowy liczbą wierzchołków' kopca-drzew^ra H a * — ^(ⁿ)?

Niech -^(^n) oznacza złożoność czasown algorytmu HeapDestroy dla danych rozmiaru n, w średnim przypadku, mierzoną liczbą przestawień wierzchołków' konstruowanego kopca-drzew^ra, wtedy: ^J4(^n)^= )	i	+
Niech -^(^n) oznacza złożoność czasową algorytmu HeapDestroy dla danych rozmiaru n, w każdym przypadku, mierzoną liczbą porównań etykiet wierzchołków' konstruowanego kopca-drzew^ra, wtedy: ^=	0
Niech -^(^n) oznacza złożoność czasown algorytmu HeapDestroy dla danych rozmiaru n, w każdym przypadku, mierzoną liczbą przestawień wierzchołków' konstruowanego kopca-drzew^ra, wtedy: 'R(ri) = o{r\2)	1	+	+

Rozważmy algorytm HeapSeąuence postaci:

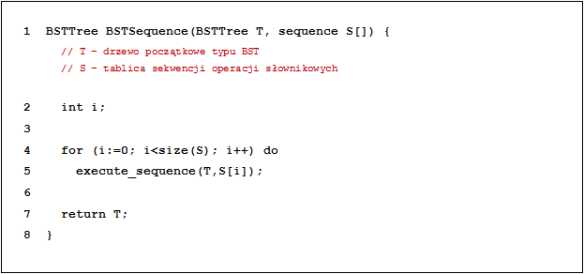
Niech kopiec H będzie rezultatem działania algorytmu HeapDestroy dla danych wejściowych:

•    kopiec-drzewo początkowy ^H = Hea/>Pa.sf£7<>n.st™cf([0,3,6,10,14,17,5,16,l,7])_{s gdzie} ajgo^ HeapFastConstract jest szybkim algotytmem budowy kopca-drzewa,

•    sekwencja operacji kolejki priorytetowej S :

1 DELMIN (INSERT (H,MIN (ff)))

2. DELMIN(INSERT(H, 18))

3    DELMIN(INSERT(H,MIN(H)))

4    delmin(insert(h,min(h)))

5    INSERT(H,MIN(H))

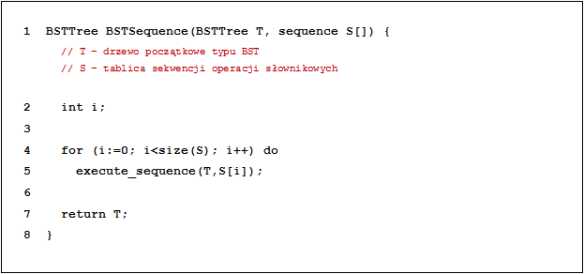
Które z poniższych zdań jest prawdziwe?

Maksymalna wysokość kopca-drzew'a binarnego H w trakcie wykonania przedstawionego ciągu operacji jest równa dokładnie 3	i	+
Ostateczna liczba wierzchołków kopca-drzew^ra binarnego H tuż po wykonaniu przedstawionego ciągu operacji jest równa dokładnie 11	i	+
Ostateczna wysokość kopca-drzew^ra binarnego H tuż po wykonaniu przedstawionego ciągu operacji jest równa dokładnie 2	0

Rozważmy algorytm HeapSeąuence postaci:

Które z poniższych zdań jest prawdziwe jeżeli jeżeli n jest początkową liczbą wierzchołków' kopca-drzewa binarnego H a ^Size{5) — <9(n)?

Niech ^(^n) oznacza złożoność pamięciown algorytmu HeapSeąuence (implementacja iteracyjna operacji kolejki priorytetowej) dla danych rozmiaru n, wtedy: l°gn)	0		+
Niech oznacza złożoność czasown algorytmu HeapSeąuence dla danych rozmiaru n, w pesymstycznym przypadku, mierzoną liczbą porównań etykiet wierzchołków' drzew^ra, wtedy: Vy(n) = o{2i)	1	+	+
Niech -^(^n) oznacza złożoność czasown algorytmu HeapSeąuence dla danych rozmiaru n, w każdym przypadku, mierzoną liczbą porównań etykiet wierzchołków' kopca-drzew'a, wtedy: = O(log^n)	0

Rozważmy algorytm HeapSlowConstruct (wolnej budowy kopca-drzew^ra binarnego) postaci:

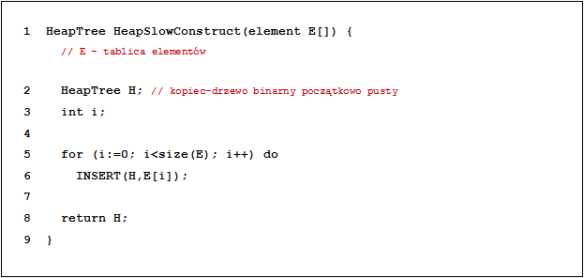
Niech kopiec H będzie rezultatem działania algorytmu HeapSlowConstruct dla danych wejściowych: • tablica elementów S = [13,14,17,10,7,9,4,6,1,2]

Które z poniższych zdań jest prawdziwe?

Wysokość kopca-drzew^ra H jest równa dokładnie 2	0
Etykiety wierzchołków' kopca-drzew^ra H wypisane w kolejności InOrder tworzą ciąg: 14,6,10,2,13,17,1,4,7,9	0
Liczba operacji porównań elementów' kopca-drzew'a wykonanych w trakcie jego budowy jest równa dokładnie 21	0

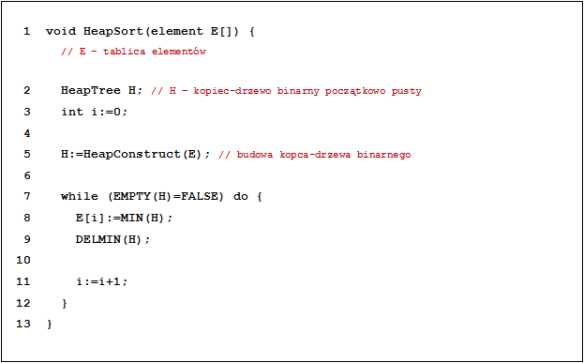
Rozważmy algorytm HeapSort postaci:

gdzie procedura składowa HeapConstuct jest implementacją algorymtu HeapFastConstruct (szybki algorytm budowy kopca-drzew^ra binarnego). Które z poniższych zdań jest prawdziwe, jeżeli *i**[E) = n?

Niech ^(^n) oznacza złożoność czasown algorytmu HeapSort dla danych rozmiaru n, w pesymstycznym przypadku, mierzoną liczbą porównań etykiet wierzchołków' konstruowanego kopca-drzew'a, wtedy: H^(n) = 0(loglogn)	0		+
Niech -^(^n) oznacza złożoność czasown algorytmu HeapSort dla danych rozmiaru n, w każdym przypadku, mierzoną liczbą porównań etykiet wierzchołków' konstruowanego kopca-drzew'a, wtedy: T(n) = l7{Ą )	0
Niech ^(^n) oznacza złożoność pamięciową algorytmu HeapSort (implementacja rekurencyjna operacji kolejki priorytetowej) dla danych rozmiaru n, wtedy: -^(^n)^= f?(l00 )	0
		System edakac	yjny. PJWSTK 2001-2007