img311 (2)

oprowadzenie do techniki sieci neuronowych 305

Ramka 9.

Uczenie sieci jako minimalizacja funkcji błędu

Celem procesu uczenia jest uzyskanie zgodności między wyjściem neuronu yU) a wymaganą odpowiedzią dla każdego przykładu zawartego w ciągu uczącym. Gdyby nie wprowadzono tego ograniczenia wówczas sieć, której na przykład nakazano rozpoznawać litery, bardzo chętnie znajdzie “rozwiązanie” polegające na tym, że absolutnie każdy pokazany obiekt będzie “rozpoznawała” jako literę A. Wprawdzie w wielu przypadkach będzie się myliła, ale za to jak wspaniale będzie rozpoznawała A niezależnie od tego, jakim charakterem pisma będzie napisane!

Podany przykład nieprawidłowego działanie sieci jest w oczywisty sposób absurdalny¹, jednak doświadczenia z sieciami neuronowymi pokazują, że mają one niewiarygodną zdolność do znajdowania “rozwiązań” polegających na minimalizacji wysiłku wkładanego w rozwiązywanie postawionych zadań i żadne środki ostrożności nie są tu nadmiarowe.

Dlatego podczas uczenia sieci tak definiujemy miarę błędu, zwaną funkcją kosztu, funkcją kryterialną lub funkcją błędu, by uwzględniała zachowanie sieci podczas wszystkich pokazów zadań wchodzących w skład ciągu uczącego:

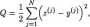
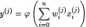
Funkcja Q jest powszechnie znana z metody najmniejszych kwadratów i jest tu adaptowana do potrzeb procesu uczenia sieci. Funkcja ta dla 7-tego kroku uczenia przyjmuje postać:

Mając daną miarę błędu Q możemy wprowadzić poprawkę wektora wag A W, wybierając ją w taki sposób, by zstępować maksymalnie szybko w dół po powierzchni błędu. Zgodnie z gradientową strategią procesu uczenia (gradientową minimalizacja funkcji błędu) należy zmieniać i-tą składową

pokazuje idealnie dokładną godzinę, ale tylko dwa razy na dobę. W tym drugim przypadku chodzi o zegarek, który wcale nie chodzi.