kinematykaw 00002

40kin

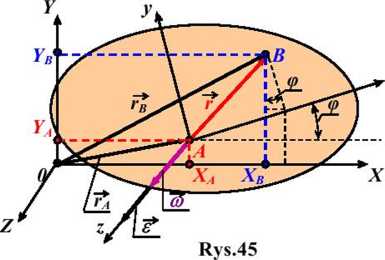
Ruch dowolnego punktu B figury płaskiej w układzie

nieruchomym opisujemy za pomocą promienia wektora r_B ->

r_B = r_A+ r

Prędkość punktu B

- dr_R    dr₄ dr

V_R = —«=^1 + — —(a)

dt    dt    dt

Ponieważ wektor"?" nie zmienia długości, zmienia tylko kierunek obracając się z prędkością kątową CO = <f) i przyśpieszeniem kątowym e = $, stąd dr _    _

dt

= CO ^x r podstawiając to do (a) otrzymujemy

(b)

V_R = V _A+a)*r = V₄ +

y z

gdzie r_x = X_B- X_A, r_y =Y_B- Y_A, r_: = Z_B- Z_A

Vb = [^vax-co{y_B-rJF + far + <o(X_B-X_A)]j

stąd składowe prędkości w układzie nieruchomym są:

Vbx    =Vax-<»(Yb ~Y_a),y_Br=Y_Ar + ®(*₈

Yb

² +v²

BY