lastscan6 (22)

76

Tablica 5.7 (cd.)

Lp.	Charakterystyka materiałów warstwy istniejącej nawierzchni	Wartość XQ
18	Żwiry i pospółki o WP <■ 30	0,70
19	Piaski grube o WP c 30	O ve 0
20	Piaski średnie 0 WP < 30	0,50
21	Piaski dtobne 0 tVp < 30	0,40

gdzie wszystkie oznaczenia we wzorze (5,13) są takie same jak we wzorach poprzednich.

Wartość liczbową N _    oraz    i H _ , . oblicza sią

z proj.    zwym, z ist,

oddzielnie dla każdego odcinka jednorodnego z uwagi na rozkład ugiąć pomierzonych. Podział trasy drogowej na odcinki jednorodne bardzo szczegółowo omówiono w dalszej części pracy. Tak więc^_zproJ₎

poszczególnych odcinków jednorodnych z uwagi na rozkład ugiąć pomierzonych istniejącej trasy drogowej nazywamy zastąpczą projektowaną grubością miarodajną, którą oznaczamy symbolem ^if’’_rproj°^d’*

Mając ustalone ^_Zp^Qj°^* dla poszczególnych odcinków trasy

drogowej można zaprojektować pogrubienie nawierzchni, wychodząc z następującej zależności:

^ miarod. r proj.

h + yh₂ + zh₃

(5.14)

z zachowaniem minimalnej grubości

i /?₂ podanych na rys.

5.1.

We wzorze (5.14) poszczególne symbole oznaczają:

' — rzeczywista grubość wzmocnienia bitumicznej warstwy jezdnej w cm,

/?2    - rzeczywista grubość wzmocnienia górnej warstwy podbt

dowy w cm,

— rzeczywista grubość wzmocnienia dolnej warstwy podbu dowy w cm,

x,y,z — współczynniki materiałowe, których wartości liczbowe odczytuje się z odpowiednich tablic jak przy projektowaniu nawierzchni nowych.

Należy wyraźnie podkreślić, że warstwę przy wzmocnieniu

nawierzchni projektuje się tylko wtedy, gdy największe możliwe do wykonania grubości + /?2 nie spełniają nierówności (5.14),

Uwzględniając tę uwagę wzór (5.14) przybiera postać:

(5.15

⁺ y^h2

max    max

gdzie:    i    oznaczają maksymalną grubość wzmocnienia

max    max

warstwy jezdnej (/?.    ) i górnej warstwy podbudowy {h-    ), zaś

max    max

pozostałe oznaczenia są takie same jak we wzorach poprzednich.

a)	dla	ruchu	lekkiego	h 1	ŚS 2	cm
b)	dla	ruchu	lekkiego i lekko średniego		^ 3	cm
c)	dla	ruchu	średniego	\	4	cm,
d)	dla	ruchu	ciężkiego	\	3*5	cm,
e)	dla	ruchu	bardzo ciężkiego		ił 6	cm,

Przy projektowaniu wzmocnienia należy pamiętać, że całkowita grubość bitumicznej warstwy jezdnej (wzmocnionej konstrukcji nawierzchni drogowej) powinna wynosić:

Przykład. Zaprojektować wzmocnienie Istniejącej nawierzchni--odcinka drogi paristwowej, przebiegającej przez południową część Polski w obszarze zagospodarowania rolniczego. Przekrój poprzeczny istniejącej nawierzchni drogowej, ustalony na podstawie wykonanych odkrywek, przedstawiono na rys. 5.2.

Zależność (5.11) możemy napisać w postaci:

i-n

U,

z ist.

Z*.

I - 1

/?

0.6 6

ist.

(5.12)

gdzie:

0.6

'ist.

Jeżeli różnica /V

z wym. i nazywamy

-    współczynnik materiałowy dla i-tej istniejącej nawierzchni ,

-    grubość    warstwy istniejącej nawierzchni dro

gowej,

-    liczba warstw is(ńiiejącej nawierzchni drogowej.

H _z^_st > O, to różnicą tą oznaczamy

przez H ^ p_roj i nazywamy zastąpczą projektowaną grubością potrzebnego wzmocnienia przeliczonego na tłuczeń standardowy, czyli możemy napisać

H

z proj.

u    _ u

z wym. "zist.'

(5.13)

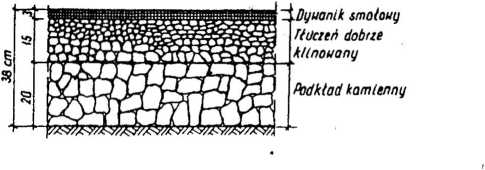
Rys. 5.2. Konstrukcja istniejącej nawierzchni drogowej