str196 (3)

196. 3. PRZEKSZTAŁCENIE LAPLACE’A I JEGO PEWNE ZASTOSOWANIA S 7. RÓWNANIA CAŁKOW

196. 3. PRZEKSZTAŁCENIE LAPLACE’A I JEGO PEWNE ZASTOSOWANIA S 7. RÓWNANIA CAŁKOW

Stosując do obu stron równania (11) przekształcenie odwrotne Laplace’a, mamy

(12)    y = L-¹ [tf (S)]+L"¹    <t> (S)l.

Na mocy wzoru Borela (3.9), mamy

(13)

Uwzględniając wzór (13) w równaniu (12), otrzymujemy

(14)

Prawą stronę równania (10) przekształcamy do postaci

UD

y =    ¹ [* (S)]+u¹ \^Z\) * L-¹ [* (S)].

Ze związku (7) wynika, że

(15)    L-¹[4>(S)] = /(0.

Z tablicy przekształceń Laplace’a odczytujemy

(16)    L-^^-^sinhU

Podstawiając wzory (15) i (16) do równania (14), otrzymujemy

(17)    y = ’/(0+/(0*sinhr.

Na mocy definicji splotu mamy

t

(18)    /(f)*sinhf = J/(f—r)sinhrd-r.

o

Podstawiając wzór (18) do równania (17), otrzymujemy szukane rozwiązanie równania (1)

t

(19)    y = /(0+ J/(f—T)sinhrdr.

o

Zadanie 7.2. Znaleźć rozwiązanie równania

t

(1)    y(/) = cos/—2j’cos(/ — t)¹ y(z)dr.

o

Rozwiązanie. Zauważmy przede wszystkim, że zgodnie z definicją splotu mamy

t

(2)    Jcos(t—-c)y(x)dr = cost*y(t).

o

Podstawiając wzór (2) do równania (1), mamy

(3)    y(/) = cost—2[cosf*y(t)].

Stosujemy teraz do obu st jego liniowość, otrzymujemy

(4)    L( Na mocy wzoru Borela (3.8)

(5)    L Podstawiając wzór (5) do ró'

(6)    L( Z tablicy przekształceń Lapla

(7)

Podstawiając związek (7) do

i

Stąd zaś

(8)

Rozkładając prawą stronę (8'

(9)

Stosując do obu stron róv

(10)

}’ =

Z tablicy przekształceń Lapla

(U)

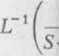
Podstawiając związki (11) d< nania (1)

Zadanie 7.3. Znaleźć rozv

(1)

przy warunku początkowym (2)