image127

38 3. Badania podstawowych właściwości fizycznych i identyfikacja tworzyw sztucznych

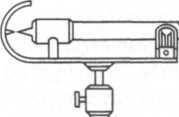
Rys. 3.5. Waga Westphala-Mohra z odważnikami

działce od 1 do 9 oznacza odpowiednie dziesiętne części zmierzonej gęstości. Drugi konik B jest 10 razy lżejszy od pierwszego, podaje zatem setne części gęstości, trzeci C - tysięczne, a czwarty D - dziesięciotysięczne.

Wykonanie pomiaru. Do suchego cylindra nalewa się badaną ciecz do poziomu, do jakiego sięgała woda przy kontroli wagi (zwykle w temp. 23°C). Następnie suchy pływak zanurza się w badanym płynie i przez odpowiednie dobranie koników sprowadza wagę do położenia równowagi. Wieszanie koników rozpoczyna się od konika największego. Jeżeli zachodzi potrzeba zawieszenia dwóch koników na tej samej podziałce, to wiesza się tylko jeden, a następny zawiesza się na koniku pierwszym. Na przykład jeżeli konik A znajdował się na podziałce 8, konik B - na podziałce 4, konik C-na podziałce 7, a konik D - na podziałce 9, to znaleziona gęstość wynosi 0,8479 g/cm³. Jest to dokładność trudna do uzyskania za pomocą areometru.

Oznaczanie gęstości cieczy za pomocą piknometru. Przy oznaczaniu gęstości cieczy należy przestrzegać wszystkich wskazówek podanych przy oznaczaniu gęstości ciał sypkich.

Wykonanie pomiaru. Suchy piknometr po zważeniu na wadze analitycznej napełnia się badaną cieczą i waży ponownie. Gęstość oblicza się ze wzoru

m₂ -m,

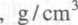
(3.10)

gdzie: m_t - masa pustego piknometru, g; m₂ - masa piknometru z cieczą, g; V-objętość nominalna piknometru zaznaczona na jego ściance, cm³.

Jeżeli piknometr nie jest cechowany, to należy go wycechować przy użyciu wody. W tym celu oprócz poprzednich pomiarów oznacza się masę piknometru napełnionego wodą w określonej temperaturze. Objętość oblicza się ze wzoru

V =

m₃ - m | P«

cm'

(3.11)

edzie: W3 - masa piknometru z wodą, g; m\ - masa piknometru pustego g; p, - gęstość wody w danej temperaturze odczytanej z tabel, np. w 23°C gęstość wody wynosi 0,997 538 g/cm³. Gęstość badanej cieczy oblicza się ze wzoru

p = —2—— p_t, g/cm³ (3.12)

wi₃ - m,

gdzie znaczenie poszczególnych symboli jest identyczne jak we wzorach (3.10) i (3.11).

3.2. Gęstość pozorna

3.2.1. Pojęcia podstawowe

Gęstość pozorna p_p jest to masa jednostki objętości danego materiału określona

wzorem

P_p = g/cm³ (3.13)

gdzie: m - masa próbki, g; V_c - całkowita objętość próbki, cm³, w praktyce często wyraża się ją w kg/m³.

Jak widać, pod względem formalnym wzór na gęstość pozorną nie różni się od wzoru na gęstość. W rzeczywistości jednak zgodność wartości liczbowych obu tych wyrażeń zachodzi tylko dla ciał nie zawierających porów, a więc całkowicie litych. Pory w czasie oznaczania gęstości metodą hydrostatyczną lub w cylindrze miarowym ulegają częściowo wypełnieniu cieczą. Przez V_c rozumie się całkowitą objętość próbki wraz z porami, co wynika zresztą z techniki wykonania opisanych niżej pomiarów.

3.2.2. Praktyczne znaczenie pomiaru

Gęstość pozorna jest cechą często wykorzystywaną w materiałoznawstwie, szczególnie w przypadku tworzyw, które ze względu na porowatą strukturę charakteryzują się istotną różnicą między gęstością a gęstością pozorną i w związku z tym rzeczywista gęstość w niedostatecznym stopniu obrazuje ich właściwości użytkowe - objętość jaką zajmą w transporcie, podczas składowania itp. Przyjmuje się, że gęstość pozorna jest najprostszym, aczkolwiek przybliżonym wskaźnikiem właściwości termoizolacyjnych tych materiałów (tab. 3.7).