Image56 (10)

110

d²x

dt²

Spg (l + Id) 2dm

x =

— co²x,

stąd

T =

2n

a>

= 2n

Spg (/ -1- 2d)

2 dm

2.53. Pod wpływem ciężaru pierwsza sprężyna ulegnie wydłużeniu x_t, druga sprężyna - wydłużeniu x₂, zaś cały układ wydłużeniu o

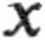
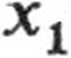
+ *2-

Przypisując układowi zastępczy współczynnik sprężystości k możemy napisać

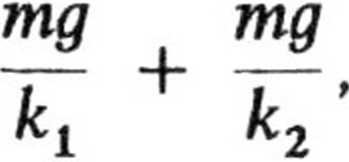
mg

k

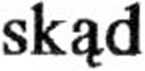
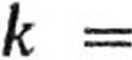
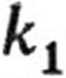
k_x + k

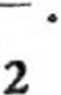
Wobec tego okres drgań ciężarka

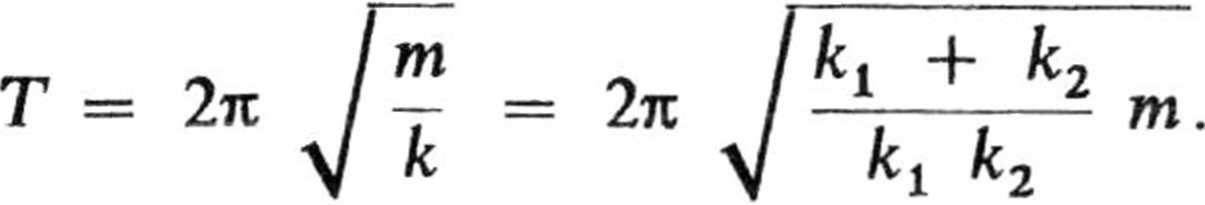
2.54. Oznaczmy przez x_t wysokość, na jaką przemieściła się ciecz w ramieniu I, zaś przez x₂ wysokość, na jaką przemieściła się ciecz w ramieniu II (rys.35).

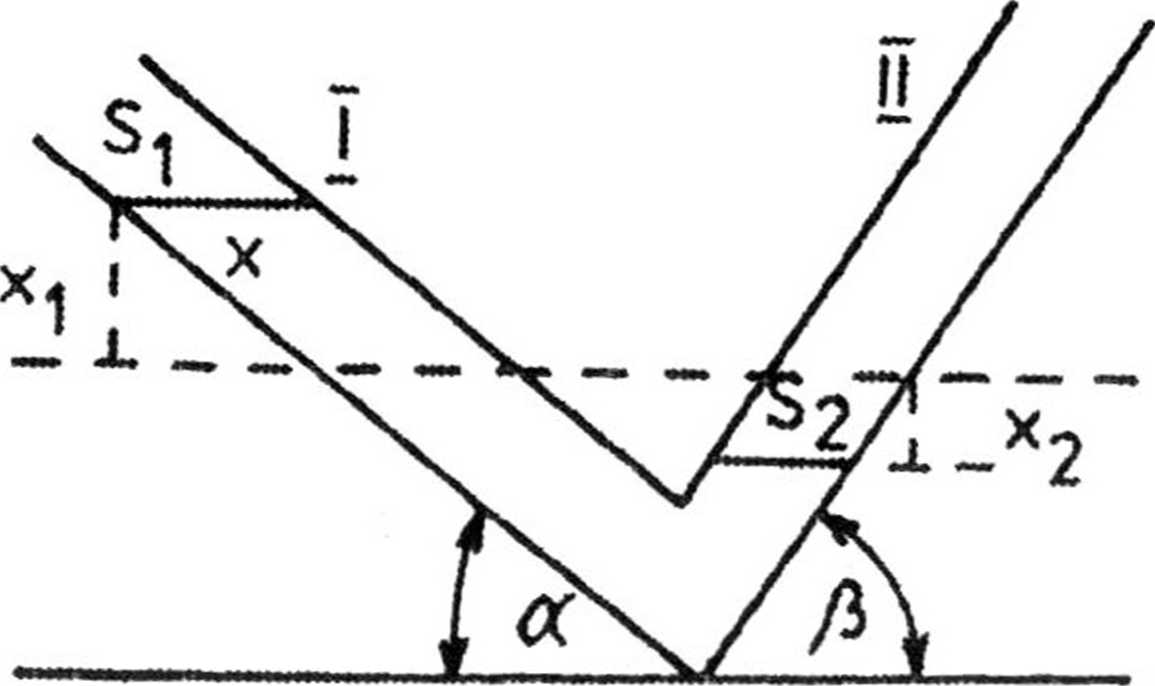
Rys.35

Wtedy niezrównoważony słup cieczy ma wysokość x_L -f x₂. Stąd siła działająca na ciecz

mg

l

F = -

(*i + x₂).

Z rysunku mamy:

S = S_{ sina = S₂ sin fi,

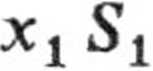
x₂ S

C

}

oraz

C

x_x = x sina,

gdzie i S₂ są swobodnymi powierzchniami cieczy, odpowiednio w ramieniu I i II, S jest przekrojem rurki. Wobec tego

F = —

mg

l

(sina + sin/i) x

i

Równanie ruchu ma zatem postać

d²x

dt²

g (sina + sinp)

/

— (l)²X.

Stąd okres drgań

T =

2n

co

= 2 71

^ (sina -f- sin/i)

/

2.55

a =

1

T

In 2 = 1,39 [s"¹],

T₀ = 0,497 [s]

2.56. Amplituda zmaleje 7,39 raza.

2.57

a. W tym przypadku równanie ruchu przybiera postać

x + 2ax + co² x = 0,

gdzie o jest stałą tłumienia, zaś co częstością drgań nietłumionych. Ponieważ ruch jest okresowy, to zachodzi przypadek słabego tłumienia i rozwiązanie równania ruchu możemy przedstawić następująco

C e ^at sin(co₁t 4- <p).

I