Image56

110

d²x

dt²

Spg (/ + 2d) 2dm

x =

co²x,

stąd

T =

2tc

co

=    2 TC

Spg (l + 2</)

2dm

2.53. Pod wpływem ciężaru pierwsza sprężyna ulegnie wydłużeniu , druga sprężyna - wydłużeniu x_z, zaś cały układ wydłużeniu o

x = x₁ + x

Przypisując układowi zastępczy współczynnik sprężystości k możemy na-

•    f

pisać

mg

k

mg mg

K k₂ '

skąd

k =

ki k₂

k_i + k

Wobec tego okres drgań ciężarka

T = 2k

m

k

2n

k_y -f k ^ki k₂

m

2.54. Oznaczmy przez x_x wysokość, na jaką przemieściła się ciecz w ramieniu I, zaś przez x₂ wysokość, na jaką przemieściła się ciecz w ramieniu II (rys.35).

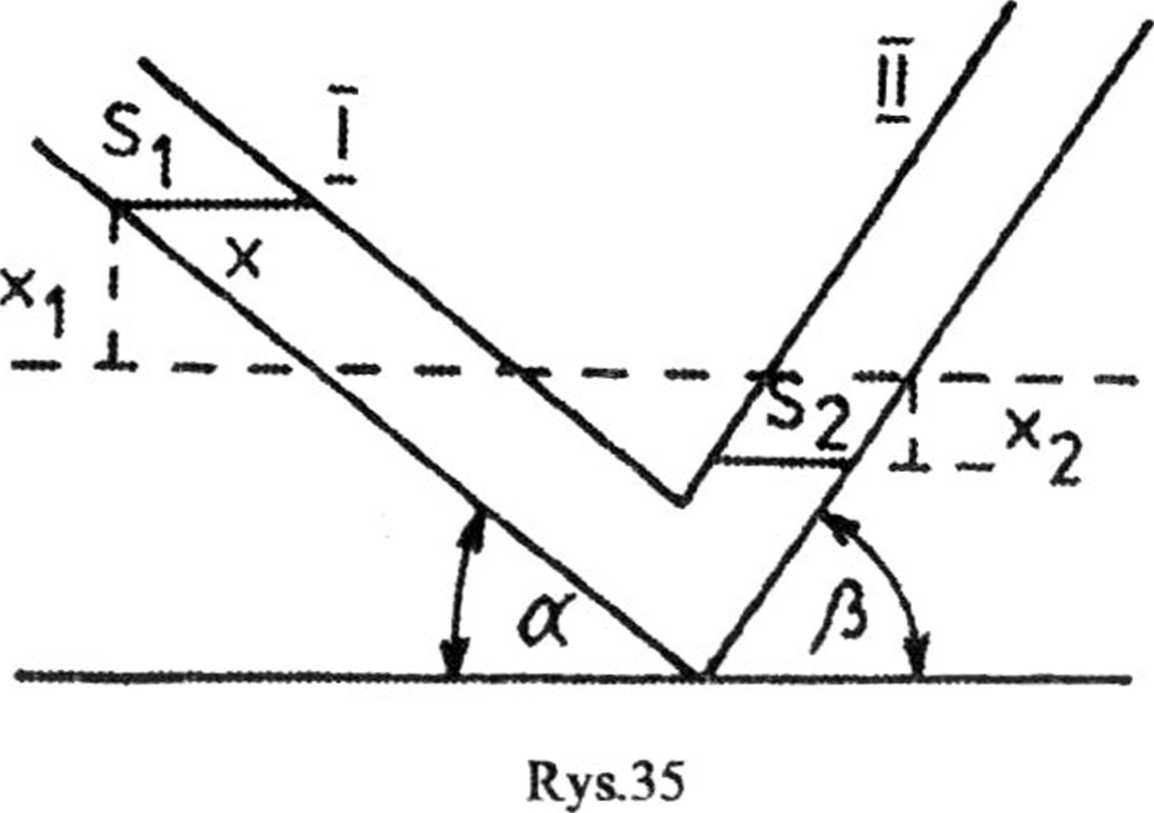
Wtedy niezrównoważony słup cieczy ma wysokość x_l + x₂. Stąd siła działająca na ciecz

mg

l

F =

(x, + x₂).

Z rysunku mamy:

S = S_t sina = S₂ sin/i,

*lSl ⁼ X2 $2 >

!

r

oraz

r

x₁ = x sina,

gdzie i S₂ są swobodnymi powierzchniami cieczy, odpowiednio w ramieniu I i II, S jest przekrojem rurki. Wobec tego

i

i

F = — —y (sina + sin/i) x.

Równanie ruchu ma zatem postać

d²x

1?

g (sina + sinp)

l

Stąd okres drgań

T =

2 n

co

= 2k

g (sina -f sin fi)

l

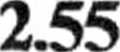
o —

1

T

ln 2 = 1,39 [s"¹],

T_a = 0,497 [s]

2.56. Amplituda zmaleje 7,39 raza.

2.57

a. W tym przypadku równanie ruchu przybiera postać

• •    m    ^

x -f 2ax + co x = 0,

gdzie o jest stałą tłumienia, zaś w częstością drgań nietłumionych. Ponieważ ruch jest okresowy, to zachodzi przypadek słabego tłumienia i rozwiązanie równania ruchu możemy przedstawić następująco

x = C e~^at sin(co₁t + (p).

I