Img00283

287

Cząstka zostanie „schwytana” przez pole i rozpocznie zataczać krąg (lub jeśli prędkość v miała składową równoległą do B, poruszać się po torze śmbowym) wokół linii sił pola magnetycznego z częstotliwością zwaną częstotliwością Larmora

= — [1/s]    (5.10-2)

^me

Jeśli wirujący ładunek elektryczny potraktować jako elementarną pętlę prądową, łatwo się przekonać, że „prąd” płynący w pętli będzie indukować w jej wnętrzu pole magnetyczne o indukcji B_jt skierowane przeciwnie do zewnętrznego pola magnetycznego (rys. 5.10-1).

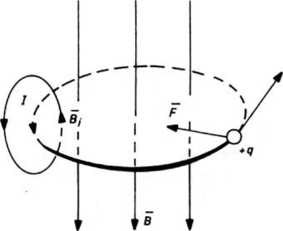
Rys. 5.10-1. Ruch cząstki naładowanej o ładunku q w polu magnetycznym

5.11. Z podobną sytuacją mamy do czynienia gdy atom znajdzie się w zewnętrznym polu magnetycznym. W zależności od kierunku wirowania elektronu wokół jądra ruch jego będzie wzmacniany lub osłabiany przez pole magnetyczne. Wielkość dipolowego momentu magnetycznego elektronu będzie zmniejszana, gdy zwrot jego pokrywa się ze zwrotem wektora indukcji pola magnetycznego, a zwiększana gdy jest mu przeciwny. W obu więc przypadkach działanie zewnętrznego pola magnetycznego jest osłabiane.

Oznacza to, że kierunek zmian prędkości kątowej elektronu pod wpływem zewnętrznego pola magnetycznego jest zawsze taki, że podatność magnetyczna jest ujemna.

Efekt indukowania dipolowych momentów magnetycznych A m przez zewnętrzne pole magnetyczne występuje we wszystkich materiałach, niezależnie od tego czy są one obdarzone trwałymi momentami magnetycznymi czy też nie.

Efekt ten jest stosunkowo niewielki, gdyż częstotliwość Larmora jest rzędu 10¹¹ rad/s, a prędkość kątowa obiegu elektronu wokół jądra jest rzędu 10¹⁵ rad/s. Podobne relacje istnieją między wielkościami Am i m_Q. O ile wektory m_Q o przeciwnych zwrotach (tj. dla elektronów o przeciwnych kierunkach wirowania) mogą się w materiale całkowicie kompensować, to indukowane momenty magnetyczne A m dodają się.