IMG�30 (2)

ści U(IJ napięcia chwilowego w chwilach r, Z lej techniki korzystamy, gdy potrzebujemy utworzyć obraz przebiegu funkcji Uft) napięcia w danym przedziale czasu oraz gdy zarejestrowany (utrwalony) ciąg wartości przebiegu ma być analizowany numerycznie ze względu np na widmo częstotliwości zawarte w przebiegu Coraz częściej jednak z tej techniki korzystamy również, co już nie jest tak oczywiste, gdy potrzebujemy wyznaczyć wartość np miary skutecznej napięcia okresowego ¹ Okazuje się bowiem. Ze numeryczne wyznaczenie wartości napięcia skutecznego wg (3 26) na podstawie ciągu wartości Ufti) jest współcześnie proste i może być dokładne

Ewolucję techniki pomiarowej prześledźmy na przykładne Jeszcze około dziesięć lat temu oscyloskop cyfrowy oznaczał konstrukcję o układne tradycyjnego oscyloskopu analogowego, którą dodatkowo wyposażono w bardzo przydatną funkcję rejestrowania wyniku pomiaru, która mogła być skutecznie zrealizowana w technice cyfrowej Natomiast aktualnie oscyloskop cyfrowy jest konstrukcją o układzie wyłącznic cyfrowym, tzn „lampa oscyloskopowa**¹ służy wyłącznie do wizualizacji funkcji sterowania oraz cyfrowych danych pomiarowych w postaci graficznej i alfanumerycznej, lak jak realizuje się laką funkcję na ekranie monitora komputerowego.

Cyfrowy pomiar napięcia chwilowego jako sposób pomiaru napięcia zmiennego realizowany jest przy użyciu cyfrowej techniki pomiaru napięcia stałego i zawdzięcza swoją pozycję osiągnięciom tej techniki mierzenie napięcia stałego jest dokładne, czas wykonania pomiaru jest krótki i stale jest skracany. Przy przejściu od pomiaru napięcia stałego do chwilowego powstaje do rozwiązania jeden problem - tam gdzie czas pomiaru nie może być zignorowany, trzeba „zapamiętać napięcie chwilowe"* danej chwili przez czas potrzebny na wykonanie mierzenia

Zmierzenie napięcia chwilowego (/(r,) w chwili /, z zadaną dokładnością oznacza równoczesne wyznaczenie wartości dwu wielkości wzajemnie zależnych - napięcia i czasu -z odpowiednią dokładnością Nie warto więc mierzyć dokładnie napięcia zmieniającego się w czasie, gdy czas nie jest dostatecznie dokładnie mierzony Postępuje się z zasady w ten sposób, że przyjmuje się dobrze zdefiniowany, początkowy moment czasu t₀ dla danego przebiegu i realizuje się odstępy czasu r stałe co do wielkości, tak ze chwila /, = ir. Mówimy w ukim przypadku, że czas poddany został dyskretyzacji Interesujące nas chwile można oznaczyć numerem < kolejnego okresu czasu r, a napięcie chwilowe dla chwili i, oznacza się wprost jako u, Okres dyskretyzacji nie pokrywa się na ogół z kwantem czasu, gdy czas jest odmierzany cyfrowo, bo na taki okres może składać się wiele kwantów cyfrowego odmierzania czasu (z zasady całkowita liczba kwantów) Dyskretyzacja czasu i kwantowanie (kwantyzacja) czasu me oznaczają z zasady tego samego Z tego powodu terminom „dyskretyzacja” i „kwantyzacja" nadaje się wyspecjalizowany sens (nie traktuje się jak synonimy).

Ten sam proces pomiaru napięcia chwilowego w dyskretnych chwilach czasu opisuje się tez w innym języku - mówi się o próbkowaniu napięcia (/(/), a odstęp czasu r jest wówczas okresem próbkowania, jego odwrotność - częstotliwością próbkowania, a wartości napięcia chwilowego u, nazywa się też próbkami Wprowadza się w ten sposób do miernictwa język statystyki.

Jak wiemy, wynik pomiaru napięcia z powodu błędu kwantowania jest nieokreślony w granicach ±0 5 jednostki kwantyzacji (patrz rys 3 12b). Gdybyśmy wielokrotnie mierzyli napięcie dokładnie stałe i o tej samej dokładnie wielkości, to błąd ten byłby stały i nie przekraczałby ±0.5q, choć me byłby znany co do wartości Mierząc w kolejnych chwilach na-

Jest to jakby pomiar pośredni napięcia skutecznego, a lego rodzaju metodę pomiaru omawialiśmy w części ogólnej

Jeżeli nawet jest konstrukcyjnie lampą oscyloskopową, lo użyta jest w trybie lampy monitora komputerowego (kineskopu), oznacza lo, że funkcjonuje w trybie rastrowym Pr^jęio się tak mówić Fizycznie chodzi o „zatrzymanie wielkości" napięcia chwilowego na czas mierzenia

pięcie zmieniające się nawet w sposób ciągły (w znaczeniu przebiegu „gładkiego''), otrzymamy ciąg wartości, w których zawarte będą błędy kwantowania na ogół różnej wartości, choć w przedziale ±0 5q Przypisujemy tym błędom - jak tojuZ robiliśmy poprzednio ogól nie - losową zmienność i rozkład (gęstości) prawdopodobieństwa jednostajny Przypisanie losowości robi się nie tylko dla wygody, zapewniające) prostotę opisu (modelu), ale postępowanie ma też fizyczne uzasadnienie Nigdy me jest tak, żeby mierzony przebieg fizyczny był doskonale gładki, ale nawet gdyby był, to nie ma elektronicznych przyrządów, w obwodach których nie występowałby ich własny, naturalny szum lub resztki tętnień sieciowych Choćby z tych powodów obraz przebiegu napięcia, ten który jest ostatecznie otrzymany w wyniku mierzenia, nie jest gładki, a wyniki pomiaru również z tego powodu mogą być losowo rozrzucone Powtarzając w takich okolicznościach pomiar można oczekiwać losowego rozrzutu wyników. Takie zjawisko (tzn brak gładkości obrazu przebiegu otrzymanego z pomiarów) wykorzystuje się nawet do numerycznego powiększania efektywnej rozdzielczości przyrządu W tym celu „gładkość może być nawet psuta”, żeby losowość wykorzystać skutecznie do poprawienia rozdzielczości Wielokrotne powtórzenie pomiaru w takich okolicznościach i uśrednianie w odpowiedni sposób otrzymanych wyników jest bowiem równoważne zwiększeniu rozdzielczości przyrządu o jeden, a nawet dwa bity Zastosowanie takiej procedury może być sposobem skuteczniejszym niZ konstrukcyjne powiększanie rozdzielczości przetwornika a/c.

Z dwu powodów ciąg wartości u, napięcia chwilowego przebiegu £/(/) jest dyskretny: z powodu dyskretyzacji czasu i z powodu kwantowania napięcia. Choćby z tych powodów jednoznaczne odtworzenie przebiegu pierwotnego U(l) dla każdej Chwili jest niemożliwe (pomijamy tu inne składowe błędu). Na rys 3.16 pokazano próbkowanie sinusoidy z odstępem czasu r (a) i różne sposoby odtworzenia pierwotnego przebiegu (b).

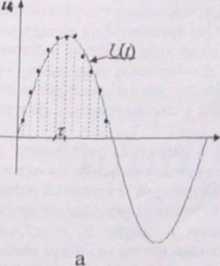
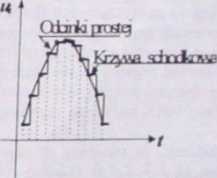
Rys. 3.16. a - Próbkowanie przebiegu sinusoidalnego co okres czasu r i b - możliwe odtwarzanie przebiegu krzywą schodkową lub odcinkami prostoliniowymi

139