kralF

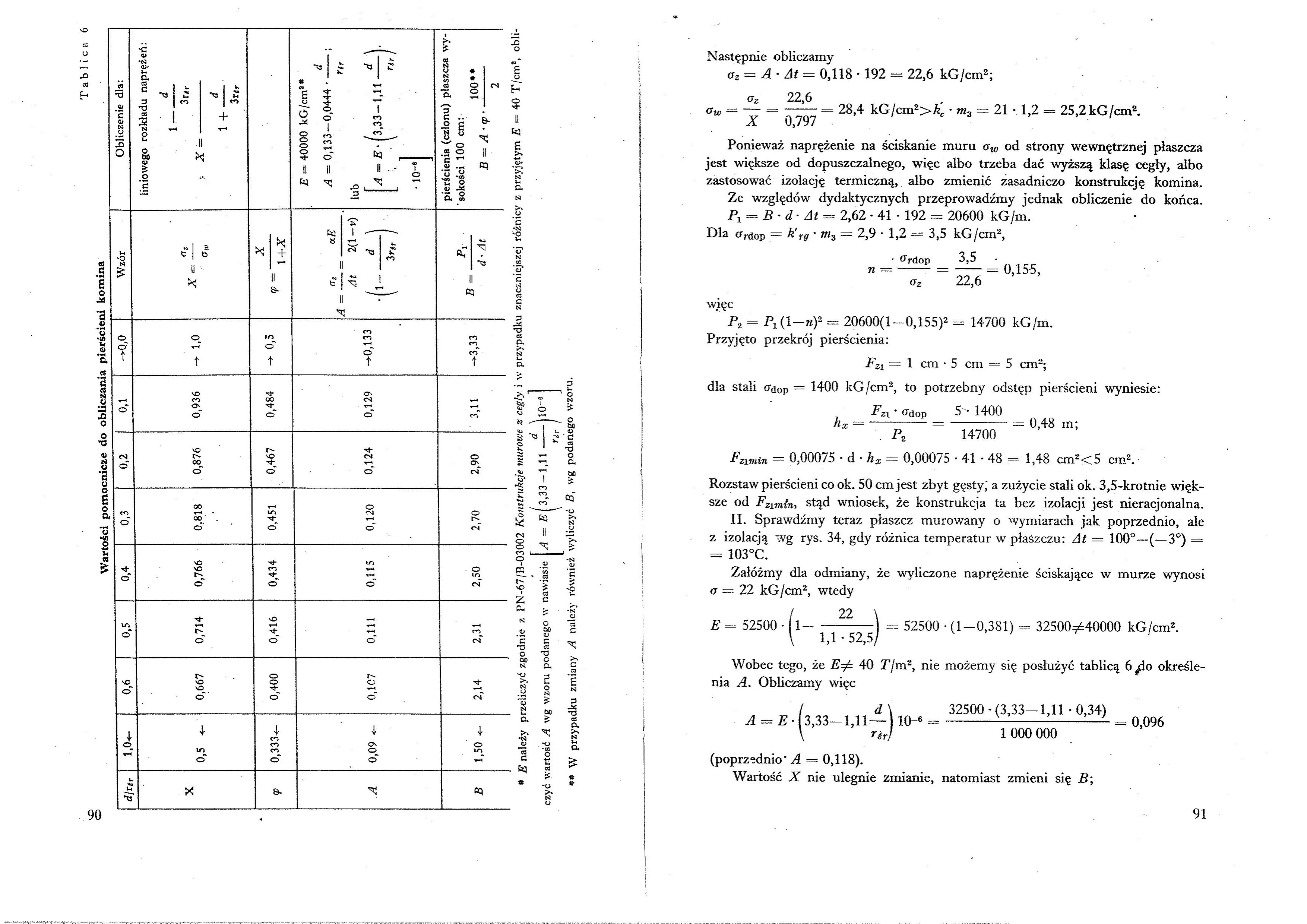
Wartości pomocnicze do obliczania pierścieni komina

Obliczenie dla:	'C <u •N <U* U a c i i *to £ "to \ u ZS 1 co I co "O | 1 + N T-» 1-H O H W >< <o ’ £ .2 c		■*1 c z s 5 .o ■*■ T O °- ^1 •* j co 8 « o 2 ? O fta ,-, II 11 II - l « J5 . ^ . T J3			pierścienia (członu) płaszcza wysokości 100 cm: 100** B = A ■ <p ■ —- 2 y z przyjętym E — 40 T/cm^2, obli-
Wzór	t | b li -■	* ± 11 8-	« to *5	1 « -b ~- 5	»r co	-2 c •N ■o < ? I "to O ■ II ej Oj % c N
CD cT t	O t	in o“ t	• co ©~ t			*2C "O co S O & CO N5 t a
o	sO co o"	•d- oo O	Os CS o			?ś' _ ^1 o T-. • N 2 & 2 l * 'T'" “
0,2	NO oo o	r* vO O	s* CS ©~			f* - ’g K ^1 T3 O 5^0 Os £ u, CS ^ co £ -i “
CO O	00 co o	to O	c CS O			h ^ ca ^04 11 --cs ^11 --o ^ >*
0,4	VD sO o	S^- CO O	en ©			2,50 \^T-67/B~030 nawiasie / również w
ITi O	>3” o	sO O	©~			^ > -S‘ <y w ^N o "3 « .2 £P ^c cs cc 03 d S O Ti
o"	sO v£^ O	o o Tł* o	r- o ©~			N O. C -r >. 2 | o 8 S 5 ^M "5 S 3 E » 3
i © TH	ł m O	1 co co co O	4 Os O ©			O. £ « 1 C* + ►» ^ £ ■N £ © _2 r? ' - J | £
| ^/P	X	8-				is • m * -0 * ^05 & O

Następnie obliczamy

a_z = A- At = 0,118 • 192 = 22,6 kG/cm²;

a_z 22,6

a_w= — =-- = 28,4 kG/cm²>£_c • m₃ = 21 • 1,2 = 25,2 kG/cm².

X 0,797    '

Ponieważ naprężenie na ściskanie muru a_w od strony wewnętrznej płaszcza jest większe od dopuszczalnego, więc albo trzeba dać wyższą klasę cegły, albo zastosować izolację termiczną, albo zmienić zasadniczo konstrukcję komina. Ze względów dydaktycznych przeprowadźmy jednak obliczenie do końca. P_l = B ■ d - At = 2,62 • 41 • 192 = 20600 kG/m.

Dla o>aop = k'_rg ■ m₃ = 2,9 • 1,2 = 3,5 kG/cm²,

3,5

22,6

0,155,

' tfrdop

n =-

O_z

więc

P._ź = Pj(I-m)² = 20600(1-0,155)² = 14700 kG/m. Przyjęto przekrój pierścienia:

F_zl — 1 cm • 5 cm = 5 cm²;

h_x

0,48 m;

dla stali Octop = 1400 kG/cm², to potrzebny odstęp pierścieni wyniesie: Fzi * Udop    5~- 1400

14700

F_zimi„ = 0,00075 • d • h_x = 0,00075 • 41 • 48 = 1,48 cm²<5 cm².

Rozstaw pierścieni co ok. 50 cm jest zbyt gęsty; a zużycie stali ok. 3,5-krotnie większe od F_zimistąd wniosek, że konstrukcja ta bez izolacji jest nieracjonalna.

II. Sprawdźmy teraz płaszcz murowany o wymiarach jak poprzednio, ale z izolacją wg rys. 34, gdy różnica temperatur w płaszczu: At = 100°—(—3°) = = 103°C.

Załóżmy dla odmiany, że wyliczone naprężenie ściskające w murze wynosi a — 22 kG/cm², waedy

E = 52500 • |l-    = ⁵²⁵⁰⁰ • (1-0,381) = 32500^40000 kG/cm².

Wobec tego, że E^ 40 T/m², nie możemy się posłużyć tablicą 6 ^do określenia A. Obliczamy więc

A = £ • (3,33—1,11—I 10-⁶ = rir)

32500-(3,33-1,11 -0,34)

1 000 000

= 0,096

(poprzednio' A = 0,118).

Wartość X nie ulegnie zmianie, natomiast zmieni się B;

91