new 83 (2)

170 7. Zasady obliczeń wytrzymałościowych śrub

bowiem oczywiste, że osiowe obciążenie robocze Q_r w gwincie sarno-hamownym nie może wywołać zmiany momentu skręcającego.

W obliczeniach projektowych, dla określenia wstępnych wymiarów śruby, można korzystać ze wzoru (7.28), w którym należy podstawić maksymalne obciążenie Q_c. Obliczone w ten sposób wymiary śruby będą bardzo nieznacznie zawyżone, gdyż w wytężeniu materiału śrub nieco mniejszy udział będą miały naprężenia skręcające niż wynikałoby to ze wzoru.

Z rozkładu sił na gwincie (patrz rys. 7.46) wynika, że istnieje moment M_0[lte = 0,5d,Qtgy starający się obrócić (odkręcić) nakrętkę względem śruby. Momentowi temu przeciwstawia się moment tarcia na gwincie M_tg — 0,5d_s/jiQ oraz moment tarcia na powierzchni oporowej nakrętki M_tn = 0,5d_tnQ. Przy obciążeniach statycznych suma momentów tarcia M_tgĄ-M_tn jest wielokrotnie większa od momentu M_odk, co stanowi dostateczne zabezpieczenie przed samoczynnym luzowandem nakrętki.

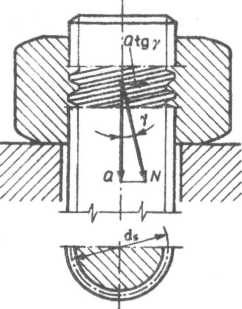
Rys. 7.46. Rozkład sił czynnych działających na nakrętkę

Przy zmiennych siłach osiowych na powierzchni gwintu występują zmienne promieniowe obciążenia śruby i nakrętki. Pod wpływem sił promieniowych, a także na skutek zmiennego przewężenia przekroju poprzecznego śruby (wywołanego zmienną siłą osiową) następuje przemieszczanie gwintu śruby względem gwintu nakrętki (patrz 6.1.3 i 6.1.4). W wyniku tych mikroprzemieszczeń następuje wygładzenie powierzchni styku. Współczynnik tarcia na gwincie oraz na czole nakrętki zmniejsza swą wartość nawet do ju — 0,005. Już przy /u — 0,02 połączenie gwintowe staje się niesamohamowne (M_odk > M_tg + M_tn). Dlatego też śruby w połączeniach zmiennie obciążonych liczy się (z pominięciem skręcania) z warunku czystego rozciągania.

Naprężenia średnie i nominalną amplitudę naprężeń (patrz rys. 7.34 i rys. 7.18) określają zależności

oraz

Om

Ona

Qm	Qc+ Qw 2
Kdl	Kdl
4	4
	Qc Qw
Qa	2
~dl	icd*
4	4

(7.117)

(7.118)

Określenie współczynników uwzględniających działanie karbu (jj lub a i q) i wielkość wymiarów nominalnych gwintu pozwala na wyznaczenie rzeczywistego współczynnika bezpieczeństwa d według wzoru (7.6) lub (7.9) oraz współczynnika d_a według wzoru (7.13).

7.6. Obliczenia połączeń wielośrubowych

7.6.1. Ogólne zasady i założenia

W połączeniach dokonywanych za pomocą większej liczby śrub rozkład obciążenia na poszczególne śruby zależy od konstrukcji złącza oraz od kierunku i rodzaju przyłożonego obciążenia. W połączeniach wielośrubo-wych stosuje się zasadę, że wszystkie śruby mają takie same wymiary bez względu na to, czy są obciążone równomiernie czy nierównomiernie. W przypadku nierównomiernego rozkładu obciążenia w połączeniu, obliczenie sprowadza się do wyznaczenia obciążenia śruby najbardziej obciążonej i określenia jej wymiarów. Gdy na śruby działa złożony stan obciążeń oraz w przypadku obciążeń zmiennych wygodniej jest założyć wstępnie ich wymiary, a następnie sprawdzić rzeczywisty współczynnik bezpieczeństwa. W obliczeniach rozkładu obciążeń przyjmuje się, że płaszczyzna styku łączonych elementów (o względnie dużej sztywności) pozostaje płaska oraz że napięcie wstępne we wszystkich śrubach jest takie samo.

Wielkość napięcia wstępnego powinna być taka, aby — po przyłożeniu obciążenia roboczego — było zapewnione przyleganie łączonych elementów na całej powierzchni styku. W celu określenia tego napięcia rozpatrzmy styk złącza obciążonego siłą rozciągającą P i momentem M„ (rys. 7.47a). Dla uogólnienia rozważań przyjęto dowolne rozmieszczenie

śrub o dowolnych przekrojach F_t =-~p • Siły napięcia wstępnego w tych

śrubach są równe

Qwi — o_wF_t. (7.119)