P1010763 (3)

1SS 2. SCHODY ŻELBETOWE

m f    k    k    k    k    ~i

— COSOK+1+ r-cosak—+_r cosfln——-cos a|c a |_    *    h    n    h

-cosflk)+—(cosofi-l)j,

ponieważ a=2n//i, stąd ostatecznie otrzymamy

M_m«-(l-cosfc).    (2.₁₍₅₎

Pierwsza pochodna tego wyrażenia wobec przyjętego przedziału dla k od 0 do h Wika. żuje, że ekstremum występuje przy p=n, a więc fc=/t/2, co odpowiada połowie wysokości

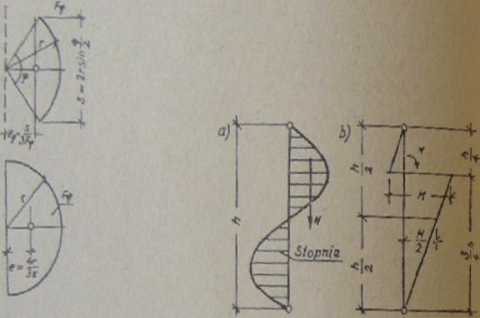
Rys. 133. Rzut stopni o kącie wewnętrznym Rys. 134. Schody spiralne: a) schemat koostruk-0<p<*    cyjny, b) wykres momentów przy kącie

słupa przy założonych warunkach brzegowych. Poszukiwany moment w słupie wyrazi się więc wzorem

m, N 2m W(*)=—(1-cosn)*— ' a a	(217)
Po podstawieniu a~2njh otrzymamy mh Mw=MnuI--- n	(2.18)
Uwzględniając równania (2.11), (2.12) i (2.13) będzie
mh hOe e _ % hm %	(2.19)

W przypadku obciążenia równomiernego (przy stałym ciężarze użytkowym i stałej grubości

płyty)

3.7. SCHODY SPIRALNE PREFABRYKOWANE

piĆ^,tt

ostatecznie, uwzględni ąjąc sumę obciążeń, otrzymujemy

M.

13

(2-21)

^ podłużną w słupie określa się jako sumę sił pionowych przekazywanych przez stopnie ^ góry (gdzie N= 0) do obliczonego przekroju. U podstawy słupa występuje maksymalna ‘^ftość siły N- £& +& (gdzie R - oznacza ciężar własny słupa, a£g, - ciężar własny ₍₀poi i użytkowy przypadąjący na stopnie). Gdy rzut stopni spiralnych ograniczony jest _tfffl mniejszym od 2rt (rys. 2.33), czyli 0<p<n, moment zginający w słupie można Je# ze wzoru

(2.22)

u}_Cs - długość cięciwy j=2rsinę>/2, q - ciężar własny stopnia i użytkowy przypadają _na stopień w kG/m².

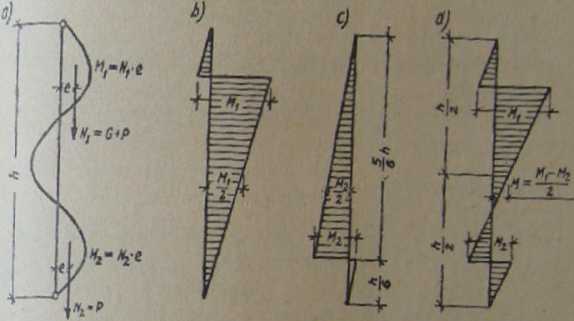
Rji 2.35. Schody spiralne: a) schemat konstrukcyjny przy kącie #=3x, b), c), d) wykresy momentów

Afj i Mt

Maksymalny moment zginający wystąpi przy ?=180^s, wówczas

M »yr² ^rsiny-q « j-r³(g+p).    (2.22a)

Gdy rzut stopni tworzy pełen okrąg, to jest przy p=2ir, (rys. 2.34a) następuje zrównoważenie momentu od obciążenia stałego i wtedy maksymalny moment, jaki wystąpi przy obciążeniu użytkowym, działąjący w połowie okręgu wynosi

$ui0Ą    (222b)

Jeżeli natomiast kąt p=3n (rys. 2.35a), to przy nieparzystej liczbie półokr^ów wykresy momentów przedstawiają rysunki 2.35b, c, d, a wartości momentów Af_? obliczamy ze wzoru (2.22a), natomiast wartości momentów \f₂ obliczamy ze wzoru (2.22b).

Przy wymiarowaniu stupa należy uwzględnić jego wyboczenic; np. przy przegubowo-■nieprzesuwnym podparciu obu końców miarodajny do obliczeń może się okazać moment w połowie wysokości słupa, jak to zaznaczono na rys. 2.35b i 2.35d.