P1010851

7. ŁUKI

7.1.2. Kształt łuków

Kształt osi łuku należy możliwie dobrać taki, aby linia ciśnień od obciążenia zasadniczego pokrywała się z osią geometryczną łuku. Wtedy wielkości momentów zginających

'

od obciążeń drugorzędnych, różnych w działaniu od zasadniczych, będą miały wartości niewielkie.

Dla obciążenia równomiernie rozłożonego na rzut linią ciśnień będzie parabola drugiego stopnia. Przy obciążeniu radialnym nąjodpowiedniejszy będzie luk o osi kolistej. Dla obciążenia hydrostatycznego linia ciśnień będzie odpowiadała krzywej łańcuchowej.

9

Oj

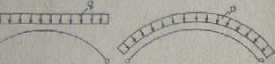
Rys. 7.6. Schematy obciążeń pionowych dla luków

Schematy poszczególnych obciążeń podano na rys. 7.6.

W konstrukcjach budowlanych nąjczęściej stosowane są luki o kształcie osi paraboli drugiego stopnia.

Łuk paraboliczny w układzie kartezjańskim posiada równanie

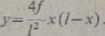
(7.1)

Ten kształt łuku znacznie upraszcza obliczenie i ze względów konstrukcyjnych jest najczęściej stosowany — ryś. 7.7. Ponieważ odchylenia między parabolą o odcinkiem koła przy małej strzałce łuku nic są wielkie, kształtuje się często łuki płaskie do///< 1/5 jako odcinki koła, co upraszcza wykonanie krążyn i deskowania.

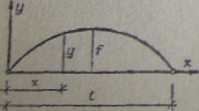
Rys. 7.7. Geometria łuku parabolicznego

Najczęściej stosowane strzałki łuków opierających się na ścianach bocznych lub słupach wynoszą

W zależności od stosunku strzałki łuku /do rozpiętości I, czyli (=f/l, rozróżniamy foki płaskie i luki smukłe. W budownictwie stosuje się najczęściej łuki o smukłości od £-0,05 ! 0,5. Łuki o {>0,20 klasyfikuje się jako smukłe, zaś przy {<0,20 jako płaskie.

7.2. METODY OBLICZANIA ŁUKÓW

Do łuków statycznie wyznaczalnych należy zaliczyć łuki swobodnie podparte stosowane zazwyczaj jako schematy zastępcze oraz łuki trójprzegubowe. Łuki te rozwiązujemy za pomocą trzech warunków równowagi    £l*0, £Af=0. Natomiast łuki sta

tycznie niewyznaczalne, podobnie jak i inne ustroje statycznie nie wyznaczał ne, należy rozwiązywać za pomocą dodatkowych warunków, tak zwanych warunków odkształceń sprężystych.

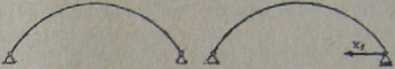
Układ podstawowy    Układ zastępczy

Rys. 7.8. Schemat obliczeniowy luku dwuprzegubowego

Układ podstawowy    Układ zastępczy

Rys. 7.9. Schemat statyczny łuku danego

Wielkości nadliczbowe w układach łukowych wyznacza się najczęściej metodą stf.

W przypadku obliczania wielkości nadliczbowych metodą sił jako układ zastępczy przyjmuje się dla łuków dwuprzegubowych, zwykle luk swobodnie podparty (rys. 7.8).

Gdy układ jest n-krotnie statycznie niewyznaczalny (rys. 7.9), równania kanoniczne metody sił w przypadku nieuwzględnienia zmiany temperatury i osiadania podpór przyjmują postać

(7.2)

*l*Il + *2*I2 + ~+*l*II*ł*u + -+*.*U + 4|»«0, ^i^21 + ^2^22 + -" + ^|Ó2| + ^f,iÓn + ...+.Af_llÓ2» + d2_J, = 0, ■^t^lt+-^2^l2 + — +^|Ó_/| + X'_tÓ_(k + ... + X_llÓ_|ł-|-d|₍, = 0,

* 1 ^1.1 + *2 2 + • • • +    + X* ó,* + . ■. + X, ó,,, + d., = 0 ,

*    *    I

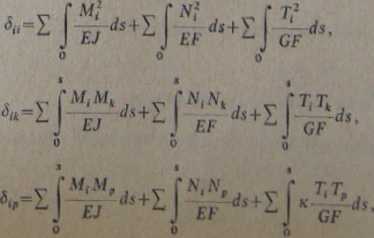
gdzie

(7.3)