P4250114

grubością warstwy przyściennej i cięciwą 5 istnieje stały stosunek tylko dla określonej pary wartości Re, kjs. Dla łopatek bardziej chropowatych lub mniejszych liczb Reynoldsa grubość warstwy przyściennej rośnie. Jeżeli więc zmniejszymy cięciwę s przy k_t = const. to wzrośnie chropowatość względna kjs i zmaleje liczba Reynoldsa Re = cs/v.

W efekcie wzrosną straty profilowe. Jednocześnie straty brzegowe zmniejszają się o znacznie mniejszą wartość od oczekiwanej bez uwzględnienia tych efektów. Nie ma więc zmniejszenia strat w stopniu, często może nastąpić wzrost strat [6]. Te rozważania tracą ważność dopiero przy bardzo dużych liczbach Reynoldsa i bardzo małych chropowatościach względnych, które nie występowały w omawianych badaniach eksperymentalnych.

Smukłe łopatki (duże l/s) są tylko wtedy korzystne sprawnościowo, gdy jednocześnie kjs jest małe oraz Re duże. Warunek ten jest spełniony dla dużych wartości s, zatem dla dużych absolutnych długości łopatek.

W przypadku krótkich cięciw s, zwiększenie smukłości drogą dalszego zmniejszenia cięciwy przy l = const mogłoby dać zmniejszenie strat, gdyby jednocześnie odpowiednio zmniejszono bezwzględną chropowatość powierzchni profilu dla utrzymania kjs = idem, a jednocześnie zwiększono liczbę Reynoldsa, np. przez zwiększenie gęstości czynnika w badaniach modelowych. Spełnienie tych warunków jest przeważnie niemożliwe.

Straty brzegowe można obliczać według wzoru [48]:

C,

Łl.jAi-r fi-

)i r

(V1.16)

gdzie straty brzegowe jednostkowe (dla - = 1) obliczamy ze wzoru półem-pirycznego:

(VI. 17)

Duży wpływ na straty brzegowe ma współczynnik

F-F(da, Co/c_Ł),

zależny od kąta odchylenia w palisadzie, Aj = 180°—(oc₀+a,), i stopnia zmiany prędkości cjc_l (rys. VI. 13).

Wartości funkcji F uzyskane na maszynach modelowych są około 2 razy większe od współczynników otrzymanych przy badaniu palisad płaskich (o czym już wspomniano). Z tego względu należy zachować ostrożność przy korzystaniu z różnych atlasów profili podających wyniki pomiarów palisad nieruchomych.

Składnik    wskazuje, że wartość podstawową funkcji F, braną

z rysunku YI.13, należy powiększać w tej samej proporcji, w jakiej strata profilowa konkretnej palisady jest większa od uzyskanej z obliczeń opartych na podanych wzorach i wykresach.

Jeżeli zastosujemy palisadę o korzystniejszych profilach, to maleje strata profilowa i jednocześnie maleje strata brzegowa, czyli korzyść jest podwójna. Natomiast mając do czynienia z palisadą chropowatą, dla której współczynnik strat profilowych

Cp ⁼ Zr‘Cp ^ Cp»

musimy uwzględnić jednoczesny wzrost strat brzegowych w tej samej proporcji

Ci =    (VU8)

Występującą we wzorach (VI. 16) i (VI. 17) podziałkę względną t/s dobieramy w zależności od typu profilu. Przy projektowaniu przyjmuje się na ogół wartości optymalne t/s = (t/s)_opl zgodnie z rysunkiem V1.9. Jeżeli t/s # (t/s)_opl, to okoliczność ta powoduje pogorszenie strat profilowych £_p > C_p, co wymaga dodatkowego uwzględnienia we wzorze (VI. 16).

Jak już wspomniano, wzór (VI. 16) obowiązuje dla łopatek dostatecznie długich, spełniających warunek l/s > (l/s)_k.

W przypadku łopatek krótkich.gdy l/s < {l/s)_k, Traupel[48] zaleca relację:

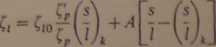
gdzie: A = 0,020 — profile przyspieszające, A = 0,035 — profile akcyjne. Ściśle biorąc, należałoby straty brzegowe obliczać oddzielnie u głowy

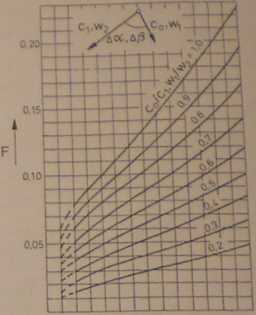
O 20    40    60 flO 100 120 U0*

AOO.A/3

Rys. V1.13. Funkcja F do obliczania strat brzegowych [48]