P5040297

>•600000

Normy wektorów i macierzy

Normy macierzowe indukowane przez normy*{\ 1 )—{13) dane są wzorami

n

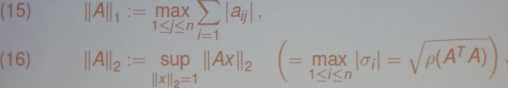
n

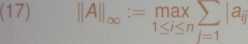
gdzie 07 są wartościami szczególnymi macierzy A a p{A^TA) oznacza promień spektralny macierzy A^TA, tj. jej największą wartość własną.

Każdą macierz Amxnmożna rozłożyć na iloczyn m    gcfa

P, Q - macierze ortogonalne, D = diag ,..., <T_mj_n(m,n))> •    dla

i < j. Elementy <r, diagonali D nazywamy wartościami szczególnymi.

■

fllfcjyiww Bftocewsfa (Poitechnika GdańaKa)    yĘTODY NUMERYCZNE AL    'j