plyta 6

Pokazana na nim powierzchnia ugiętej płyty ma równanie z = z(x,y). Rozpatrzmy sytuację w punkcie P(x.y) tej płyty. Są tu pewne nachylenia w kierunkach osi x i y. które oznaczymy literami p i ą\ odpowiadają im kąty ugięć a.f? . Zmienność tych nachyleń powoduje powstanie

krzywizn k_x.k_v oraz skręcenia powierzchni a w konsekwencji momentów zginających

** **

M_x.M_y, momentu skręcającego M_xv i naprężeń oy.oy. i z .

Wektor normalny n do płyty w punkcie P zastępujemy równoległym doń wektorem m o współrzędnych \p.q-1], charakteryzującym się tym, że jego współrzędne p,q są

pochodnymi cząstkowymi funkcji z = z(x.y), a zarazem wspomnianymi przed chwilą

nachyleniami, to znaczy

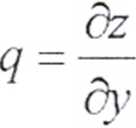
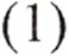
oz

P = —

ox

Płaszczyzna prostopadła do wektora Fi (czyli m) i przechodząca przez punkt P jest płaszczyzną styczną do powierzchni płyty. Jest ona wykreślona na rys. 3. Jeżeli teraz wystawimy płaszczyznę x = x₀ prostopadłą do osi x i przechodzącą przez punkt P, to

płaszczyznę płyty przetnie ona wzdłuż krzywej L zwanej linią ugięcia w kierunku osi y

(wykreślona na rys. 3).Płaszczyzna x = x₀ przecina płaszczyznę styczną wzdłuż prostej AP -

stycznej do płyty w punkcie P. Ta prosta tworzy z płaszczyzną xy kąt (3, którego tangens

nazywa się nachyleniem płyty w punkcie P w kierunku y i oznaczany literą q, to znaczy q - tg(/?). Sam kąt (3 nazywamy kątem ugięcia. Zestawiając to z (1) otrzymujemy związki

P = ą = \ZfS    (2)

dy

w'

To rozumowanie można powtórzyć dla przekroju y = y₀, tzn. płaszczyzny prostopadłej

do osi y. Z powierzchnią płyty przetnie się ona wzdłuż krzywej L_x (na rys. 3 nie wykreślonej)

zwanej linią ugięcia w kierunku osi x. Styczna do tej linii w punkcie P (prosta BP na rys. 3) tworzy z płaszczyzną xy kąt a zwany kątem ugięcia w kierunku x. Jego tangens jest nachyleniem płyty w tym kierunku, które oznaczamy symbolem p, to znaczy p = tga.

Analogicznie do (2) mamy w tym przypadku

P = P = tg «    (3)

ox

Pozostaje przed nami zadanie powiązania tych wielkości z obrazem prążkowym wytworzonym przez nasz układ optyczny. Powiedzieliśmy wyżej, że siatka szczelin daje obraz, którego prążki są miejscem geometrycznym punktów jednakowych nachyleń płyty. Z teorii układu wynika, że szczeliny równoległe do osi v (jak na rys. 1) dają prążki jednakowych nachyleń p: na danym prążku jednakowe są nachylenia p oraz kąty ugięć a . Ujmuje to wzór

(U _n +ks) cos e + Asinć'

p = -—-—-_:—    (4)

/₂( 1 + coss) ~{U_p + ks)sinć'

w którym

/r jest numerem (rzędem) prążka, p - nachyleniem na tym prążku,

.v - oznacza odległość między szczelinami siatki,

6