ScanImage018 (4)

mi mm mm mk mb

SVPROWADZENI C

Program 1.4. Kompresja ścieżek przez połowienie

Jeżeli zastąpimy pętle for z programu 1.3 poniższym kodem, skrócimy o połowę długość każdej ścieżki, przez którą przejdziemy. Wynik ogólny takiej zmiany jest taki, że drzewo po odpowiednio długiej sekwencji takich operacji stanic się prawie całkiem płaskie.

for (i = p; i != id*i]; i * id[i]) idlil * id[idii]1; for (j - q; j != id[j1; j = id;j)> id[j] = id(id[j1);

O 1.19. Podaj przykład ilustrujący fakt, iż modyfikacja algorytmu szybkiego scalania (progTamu 1.2) polegająca na zaimplementowaniu pełnej kompresji ścieżek (patrz zadanie 1.16) nie wystarczy, aby zagwarantować, że drzewa nic będą zawierały długich ścieżek.

• 1.20. Zmodyfikuj program 1.3 tak, aby wykorzystywał wysokość drzew (najdłuższą ścieżkę od dowolnego węzła do korzenia) zamiast ich wag (tj. liczby ich wierzchołków) do podejmowania decyzji, czy wykonać instrukcję id [ i ] = j czy id [ j ] -i. Przeprowadź testy empiryczne i porównaj ten wariant z programem 1.3.

0*' 1.21. Wykaż, żc twierdzenie 1.3 jest spełnione dla algorytmu opisanego w zadaniu 1.20.

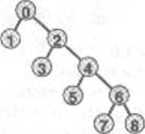
Rysunek 1.10 Kompresja ścieżek przez połowienie

Długość ścieżek prowadzących do

• 1.22. Zmodyfikuj program 1.4 tak, aby generował losowe pary liczb naturalnych z przedziału od 0 do n - 1 zamiast odczytywać je zc standardowego wejścia i działał w pętli do czasu, aż zostanie wykonanych n - 1 operacji scalania. Uruchom program dla n = 10\ l()⁴, 10* i 10^f' i podaj liczby wygenerowanych krawędzi dla każdej z wartości n.

• 1.23. Zmodyfikuj program z zadania l .22 tak. aby wypisywał liczbę krawędzi niezbędnych do połączenia n obiektów, dla 100Snś J000.

korzenia możemy skrócić prawie    ,    .

o połowę, biorąc pod uwagę po dwa •*' 1-24. Podaj odpowiedni wzór na K(n), liczbę losowych kra-

łącza naraz i zmieniając tak niższy    wędzi niezbędnych do połączenia n obiektów.

z węzłów, by wskazywał ten sam

węzeł co wyższy, jak pokazano na

rysunku. Wynik takiej operacji jest

asymptotycznie taki sam jak pełnej

kompresji ścieżek.

A

T

Rysunek 1.11 Duży przykład skutków kompresji ścieżek

Ta sekwencja opisuje wynik przetwarzania losowych par 100 obiektów przez zrównoważony algorytm szybkiego scalania z kompresją ścieżek. Wszystkie oprócz dwóch węzłów drzewa znajdują się w odległości jeden lub dwa od korzenia.

20