skanuj0017 (183)

Macierzowy zapis równań (1), (2), (3) i (4) ma postać

1	0	0
0	1	1
0	0	30
0	0	15

‘	H'		' — 6P'
	V		—8P
	R	+	— 60P
	W_		0

lub kompleksowo

Niewiadome

A-N + W_w = 0.

N = —A~¹W_w, wyznaczy się w przypadku znajomości macierzy odwrotnej A~^L, która istnieje wtedy, gdy det A #0. W omawianym przypadku detA = —75 #0.

Ponieważ warunek ilościowy został zachowany, to ustrój jest statycznie wyznaczalny.

• Siła w pręcie G.

Równania (3) i (4) można doprowadzić do

2R + JP-4P = 0, 3R + PP = 0.

Pierwiastkami tego układu równań są

R = —4P, W = + 12P,

Z równowagi węzła 2 (wcześniej analizowanego) mamy

Si

W

T

-~r= -6^/2P.

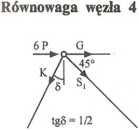
0,

ZY= 0,    Kcos5+S₁-—= = 0, Kcos5—6P

Ti

IX = 0, G+6P+SrT -Ksin5 = 0,

T

G= -6P-(-6V^)-T-+(6P/cosń)sin5,

y/1

G = — 6P+6P+6Ptgń, G = +3P,

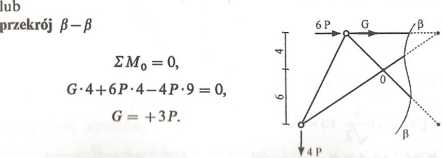
Przykład 16. W kratownicy obciążonej jak na rysunku wyznaczyć siły w prętach K, S, N. Wykorzystać znajomość reakcji.

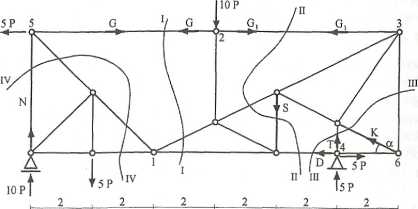
Przekrój 1-1

rM_a(/) = 0,    10P*4-5P*2-5P*4+G*4 = 0,

G— —2,5 P (ściskanie).

Równowaga węzła 2

SP_ix = 0, G—G₁ = 0, G_t = —2,5P (ściskanie).

Przekrój II-II

ZMuip) = 0, 5*4—5P*6—G_x*4 m 0, S = +5P (rozciąganie), rM_i3(p) = 0,    P*4+5P*2—5P*4—5*4 = 0, D = +7,5P (rozciąganie).

Równowaga węzła 4

IP_iy = 0,    T+5P = 0, T = —5P (ściskanie).

Przekrój ni-HI

rM_f(p), J^_x*4—5P*4+(r+5P)*4+D*4 = 0, K_x = -2,5P,

lub

K_x = Kcosa = K-^= ->K= -2,5~y/łP,

ZP_ix(p) = 0, -l^-D+SP = 0,    = —2,5P.

Przekrój IV-IV

2-M_a(0 = 0,    AM+10P*4-5P*2 = 0, N = -7,5P (ściskanie),

Uwaga: znajomość G i D pozwala wyznaczyć N i K odpowiednio równowagi węzłów 5 oraz 6.

Wyniki: /C

7,5 P.

S-+5P, N