skanuj0073 (10)

126 B. Cieślar

3.    sporządzić wykres kąta skręcenia całkowitego i jednostkowego;

4.    zaprojektować z warunku wytrzymałości i sztywności kołowy pierścieniowy przekrój poprzeczny pręta;

5.    porównać obydwa przekroje pod względem zużycia materiału;

6.    sporządzić wykresy naprężeń stycznych dla obydwu przekrojów w przekroju niebezpiecznym.

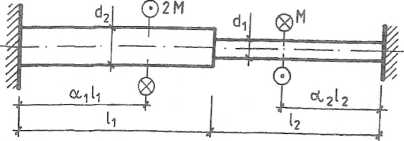
3.17. [WM-6] Dla zadanego na rys. 3.17.1 układu statycznego, należy:

1.    sporządzić wykres momentów skręcających i kąta skręcenia całkowitego;

2.    określić dopuszczalną wartość momentu obciążającego M z warunku wytrzymałości i sztywności.

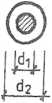
	li		ai	02	di/d2	d2	fdt	<Pd
1	1,5	5,0	0,3	0,9	1/2	15	120	1/2
2	2,0	4,5	0,35	0,85	1/3	20	110	1/3
3	2,5	4,0	0,4	0,8	1/4	25	100	1/4
4	3,0	3,5	0,45	0,75	1/5	30	90	1/5 i
5	3,5	3,0	0,5	0,7	1/6	35	80	1/6
6	4,0	2,5	0,6	0,65	1/8	40 J	70	1/8 |

Dane: li —.......	..m
fe =.......	..m
ai-.....
0-2 =......
di/d2 =.,
d2 =......	.cm
fdt -.......	..MPa
<Pd-.......... G = 8-10‘	^łMPa

Rys. 3.17.1

IV. ZGINANIE PROSTE

Zginaniem prostym nazywamy taki przypadek wytrzymałościowy, gdy w przekroju poprzecznym pręta działa tylko moment zginający, którego wektor (M_x) leży na jednej z głównych, centralnych osi bezwładności.

W tym przypadku (rys. IV-1), w przekroju poprzecznym występują tylko naprężenia normalne o, których wartość obliczamy ze wzoru:

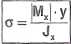
gdzie:

M_x - moment zginający,

y - odległość do punktu (współrzędna), w którym obliczamy naprężenie c,

J_x h moment bezwładności względem osi głównej, centralnej, na której leży wektor M_x.

Umowa: wektor z podwójną strzałką oznacza wektor momentu pary sił, np. M_x.

W przypadku gdy momentowi zginającemu towarzyszy stała siła tnąca, powodująca deplanację przekroju, wzór (IV-1) jest wzorem dokładnym. Jeżeli siła tnąca T nie jest stała na długości pręta, wzór (IV-1) daje wystarczająco dokładne wartości naprężeń normalnych o. Występująca również wtedy deplanacja przekroju nie wpływa jednak w sposób istotny na wartość o.

Ze wzoru (1V-1) wynika, że w danym przekroju największe naprężenia otrzymamy dla największej wartości y = ym_ax.

Iloraz

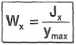
(IV-2)

nazywamy wskaźnikiem wytrzymałości na zginanie.