skrypt028 (3)

54 laboratorium Podstaw Elektrotechniki I

l*-2~    (2.4)

^Br K

2.3. Wartość skuteczna sygnałów okresowych

Wartość skuteczną sygnału fft) o okresie T określamy wzorem

to+r

F= -• \\ntf-dt    (2.5)

y ^

W przypadku gdy f(t) jest firn keją rzeczywistą wartość skuteczna wynosi:

1 ^{t0 + T}

F- -• Jf⁵(t)dt    (2.6)

! to

2.3.1. Wartość skuteczna sygnału stałego

Sygnał stały fi(t) = A można uważać za sygnał okresowy o dowolnym okresie T. Wartość skuteczna tego sygnału wynosi:

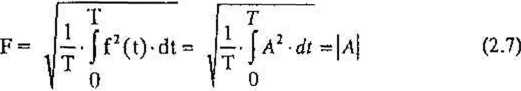
2.3.2. Wartość skuteczna sygnału sinusoidalnego

Ponieważ przy obliczaniu wartości średniej całookresowcj początek granicy całkowania można wybrać dowolnie, więc funkcję sinusoidalną przyjmujemy w postaci f(t) = A sin (rot) tzn. \|/ = 0. Wartość skuteczna takiego sygnału wyniesie:

F = JA¹ sin²(Oi dt = |a|^--J^-(l-cos2ow)-rf/=

-Mi.

4i u

t--sin2(0t

2(0

(2.8)

Tak więc dla prądu i napięcia sinusoidalnego i = t siticot oraz u - U sinrot wartości skuteczne wynoszą odpowiednio:

i
-H	(2.9)
ir u
&	(2.10)

W odniesieniu do sygnałów okresowych f(t) stosujemy dwa współczynniki charakteryzujące w pewnym stopniu odkształcenie tych sygnałów od łunkcji sinusoidalnej: współczynnik amplitudy albo współczynnik szczytu, który jest stosunkiem wartości maksymalnej do wartości skutecznej

K

(2.11)

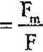
- współczynnik kształtu, który jest stosunkiem wartości skutecznej do wartości średniej półokresowej

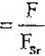
(2.12)

W przypadku sygnału sinusoidalnego współczynniki te wynoszą:

1^=72=1.41