Skrypt PKM 1 00121

242

gdzie:

4SEJ

^kes-r-

Ponieważ

J =

ad^-1 64 '

warunek powyższy zapiszemy

m¹ <5 1,702^, mi

^{dla tu =} 3S ^{= I57 [1/s]}’

d >

jm/w r

V 1,702 £    V».'

50 1 157

.702-2,1 • 10* Przyjmujemy średnicę walka d- 45 [mm].

= 43,1 [mm],

Zadanie 7.7

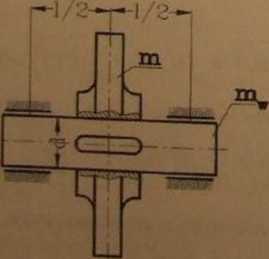
Obliczyć częstość podstawową swobodnych drgań giętnych wałka z zadania poprzedniego (zad. 7.6) uwzględniając masę wałka o średnicy d (rys. 7.22). Dane: i- 1000 [mm], d =~ 45 [mm], m = 50 [kg], >=7,8 [G/cm³], £ = 2,110⁵ [N/mm²] = 2,1 • 10¹¹ [N/m²].

Rozwiązanie

Częstość drgań bez uwzględnienia masy wałka

48 kEJ* 64 Pm

= fi. 1*11. I

m \] Pm yj

/48n-2,1-10“ 0,045*    _r._

^h V 64-i¹-50    - 201 [1/s].

Częstość drgań własnych z uwzględnieniem masy wałka obliczymy stosując wzór Raylcigha

fk

h -    —.

V

gdzie:

k — sztywność giętna wałka

48 EJ

m. - masa zredukowana

m_w - masa wałka. Ciężar wałka

0 = — h= — 100-7,8 = 15315 [G]= 153.15 [N], ^4    4

:d². nS²

Masa wałka

C ₌ Hłł? = 15,6 [kg].

9.81

Masa zredukowana

+ -«.-»+£ 15,6 = 57.8 [kg]