str142 (4)

142 3. PRZEKSZTAŁCENIE LAPLACEA 1 JEGO PEWNE ZASTOSOWANIA § I. PRZEKSZTA

142 3. PRZEKSZTAŁCENIE LAPLACEA 1 JEGO PEWNE ZASTOSOWANIA § I. PRZEKSZTA

Własność 6' (w-krotne różr również f(i), f(t), ..., f*~^l\i, yO*-D(o+o)), to ze związku L

(1.8)    L [/^<n)(0] — ^s"L[f( gdzie /^(k)(+0)= lim f^w(t),

i-*0 + 0

Własność 7 (całkowanie o

(1.9)    L[

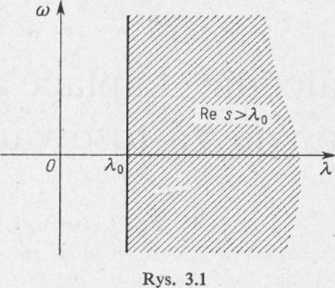
Własność 2. Jeśli <P(s) jest transformatą Laplace'a funkcji /(/), będącej oryginałem, to

lim $(s) = 0.

Rc 5 = A-»<x>

Wynika stąd w szczególności, że transformata Laplace’a oryginału /(/) nie może być postaci <P(s) = const lub <ł>(s) = s, a jeżeli jest funkcją wymierną zmiennej s, to musi być ona funkcją wymierną właściwą.

Własność 3 (jednorodność). Jeśli L(f) = <P(s), to

(1.4)    L(cf) = cL(/),

gdzie c jest stalą dowolną.

Własność 4 (addytywność). Jeśli L(/,) = <f>, (s) oraz L(J₂) = d>₂(s), to (15)    L(f₁+f₂) = L(f₁)+L(f₂).

Własność 5 (liniowość). Jeśli L(f,) = 4>,(.s) oraz L(f₂) = <P₂(s), to

(1.6)    L(^aifl+^a2fz) ^{= fl}il.(/i) + fl2^(/z)>

gdzie £ij, a₂ stałymi dowolnymi.

Własność 6 (różniczkowanie oryginału). Jeśli /'(O yes/ oryginałem (wtedy f(t) jest również oryginałem i f(0 + 0) istnieje), to ze związku L(f) = <P(s) wynika wzór

(1.7)    L[/'(Ó] = sL[/(0]-/(+0), g</z/e/(+0)= lim f(t).

l-»0 + 0

W szczególności, jeśli /(+0) = 0, to wzór (1.7) przyjmuje postać (1.7')    L [/'«)] = sL [/(»)] = s<P(s),

co oznacza, że w tym szczególnym przypadku różniczkowanie oryginału sprowadza się do wymnożenia transformaty (obrazu) przez s.

Wzór (1.9) orzeka, że całko formaty) przez s.

Własność 8 (różniczkowar

(1.10)

Wzór (1.10) orzeka, że róż nału przez (—/).

Własność 8' (n-krotne róż

(1-10')

Wzór (1.10') orzeka, że n-1 żenią oryginału przez (—1)"/".

Własność 9 (całkowanie o L [/(/)) = <P(s) wynika wzór

(1-11)

00    p

gdzie J = lim J.

a    Rc p-* co s

Własność 10 (podobieństv

(1.12) gdzie a> 0.

Własność 11 (przesunięcie

(1.13)    L[f(t-a)

Wzór (1.13) orzeka, że pn sprowadza się do wymnożenń