str121 (5)

§11. ODWZOROWANIA KONFOREMNE 121

§11. ODWZOROWANIA KONFOREMNE 121

uje obszar zakreskowany na ry-

st półosią rzeczywistą dodatnią liennej (co) bez półosi rzeczy-

z+1

1    £ =- przekształca śred-

z-1

az punktu z = 0, a więc punkt

2    przechodzi przy homografii

oczywistej (odwzorowanie jest punkt £ = —i, tzn. na półoś

urojoną ujemną. Obszar otrzymany w płaszczyźnie (0 musi leżeć w trzeciej ćwiartce, czyli mamy 7r<arg£<-§7r; funkcja w = £² odwzorowuje naszą ćwiartkę z płaszczyzny (0 na górną półpłaszczyznę zmiennej (tv).

11.    w — /l-ti . Wskazówka: funkcja £ = odwzorowuje dany obszar w płasz-

V    z— 1    z—1

czyźnie (z) w płaszczyznę zmiennej £ z cięciem wzdłuż półosi rzeczywistej dodatniej; funkcja T — \fl odwzorowuje płaszczyznę (£) z cięciem wzdłuż półosi rzeczywistej dodatniej w górną półpłaszczyznę.

12. w =    -—li-tlł. Wskazówka: por. zad. 11.11.

V    (2 + 2/)—z

13.    Na całą płaszczyznę rozciętą wzdłuż dwu odcinków 1<m<oo i —co <w< — 1 osi rzeczywistej.

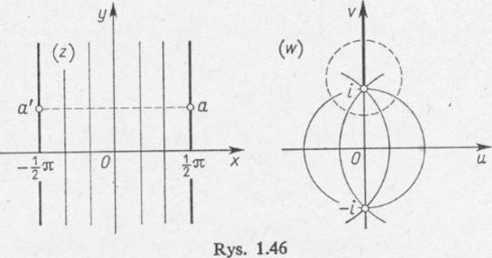
14.    Proste zawarte w pasie — i7t<Rez<^Jt i równoległe do osi Oy przechodzą w łukl okręgów

(    cos2x\²    ,    1

K + -r-r-J +0=^-5-\    sm 2xJ    sin    x

ograniczone punktami ±i. Odcinki natomiast aa' równoległe do osi Ox (rys. 1.46) przechodzą w okręgi

\    sinh 2y)    sinh    2y

pozbawione jednego punktu leżącego na osi Ov poza odcinkiem łączącym punkt + i, — i. W szczególności oś urojona Oy przechodzi w odcinek osi urojonej Ov łączącej punkty + /, —i, natomiast odcinek — i7t<x<^TC osi rzeczywistej Ox przechodzi w całą oś rzeczywistą Ou.

„ 4z+l

15. w =-, R = 2.

2+4

1    2z—3+j

^I6* ^W ~    * ~^-2+T ’ ^{R =} P^unkty symetryczne względem obu okręgów

= i (3+0, z₂ = (2+/).