76797 str107 (5)

§11. ODWZOROWANIA KONFOREMNE 107

§11. ODWZOROWANIA KONFOREMNE 107

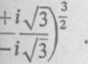
;owany (rys. 1.27) na górną izujących to odwzorowanie.

nforemnie całą płaszczyznę i z₂ = 3i (rys. 1.30) w górną

odwzorowuje punkt z_x = i w punkt £ = 0, a punkt z₂ — 3/ w punkt £ = oo. Wobec tego obszar zakreskowany (rys. 1.30) przechodzi na płaszczyznę (£) z wycięciem wzdłuż pewnej półprostej wychodzącej z punktu £ = 0.

Aby znaleźć kierunek tej półprostej, wystarczy znaleźć na niej jakikolwiek punkt różny od £ = 0. W tym celu stwierdzamy, że punktowi z = 2/ wycięcia w płaszczyźnie (z) odpowiada przy przekształceniu (1) punkt

£ = ~—~ = — 1 płaszczyzny (£).

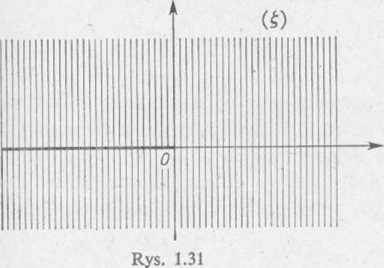
Wobec tego funkcja (1) odwzorowuje obszar zakreskowany (rys. 1.30) na płaszczyznę (£) z wycięciem wzdłuż ujemnej osi rzeczywistej (rys. 1.31). Zauważmy dalej, że przekształcenie:

(2)    T = £6” = —£

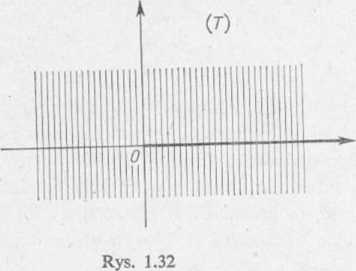
odwzorowuje płaszczyznę (£) z wycięciem wzdłuż ujemnej osi rzeczywistej na płaszczyznę (Z) z wycięciem wzdłuż dodatniej osi rzeczywistej (rys. 1.32). Aby płaszczyznę (T) z wycięciem wzdłuż dodatniej osi rzeczywistej odwzorować na górną półpłaszczyznę, wystarczy wziąć którąkolwiek gałąź przekształcenia (3)    w = Vr,

bo kąt 2n odwzorowuje się przy przekształceniu (3) w kąt

2it- i = n.

Biorąc pod uwagę wzory (1), (2), (3), otrzymujemy

Funkcja określona wzorem (4) odwzorowuje obszar zakreskowany na górną półpłaszczyznę. Jest to oczywiście jedna z funkcji realizujących to odwzorowanie. Dodajmy, że w(oo) = i, a więc punkt i nie jest obrazem punktu z obszaru zakreskowanego.

Zadanie 11.12. Znaleźć funkcję, która odwzorowuje konforemnie na górną półpłaszczyznę obszar ograniczony okręgiem C koła jednostkowego i prostą L, styczną do tego okręgu w punkcie z = i (rys. 1.33).