Str129

254 Odpowiedni do ćwfcwri

Ponieważ 2^ik ~ — 1 (niod p), możesz wykazać, żc NfVO((P ~~ 1)1** 2*) = 2*. skąd natychmiast wynika, ic p ~ l (mod 2^k+l).

(c) Jedyną liczbą pierwszą przystającą do 1 modulo 64 i mniejszą od

y/65537 jest 193. a ta liczba nie jest dzielnikiem 65537. 3. NWD(84, 1330) = 14.

I w postaci I

Pi \ P I

4. Zapisz / -

\ P

--J J i rozważ cztery przypadki ze

względu na to, jaką resztę daje p przy dzieleniu przez 8.

J!L

167

7

167

13

167

167

7

|67

13

-1

"T

-2

13

= -(-1)(-I)= “1*

6.    (a.) 14; (b) 9; (c) 9<z.

7.    a³ — a (por. dowód twierdzenia 2.2.4); 6, 60, 4080, 24, 210, 336.

8.    Ponieważ q = 1 (mod p), więc istnieje pierwiastek pierwotny f stopnia

p z jedności w ciele F_. Wtedy G = Y \ — ]ę^J ma kwadrat równy (— jp

/-i W    \PJ

(por. lemat w dowodzie twierdzenia 2.2.5).

9- (a)    T, f~pj°^J'    3126, 906 (w ostatnim przypadku skorzystaj

z równości: 1093 = (3 ⁷ — l)/2).

równy - G, jeśli p = 3 (mod 8); jest równy p+G, jeśli p = 7 (mod 8); jest równy p — G, jeśli p = 1 (mod 8).

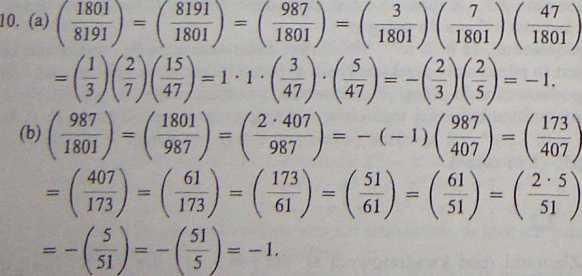
(b) Niech G= £ |j^2j| Wtedy najmniejszy dodatni pierwiastek kwadratowy z (~~JP ^modui° li - 1 jest równy (?, jeśli p = 5 (mod 8); jest

11. (a) | (b) 1; (c) 1; (d) 1; (e) 1; (f) 1; (g) -1.

11 Braflfl |    i (t)

co jest równe 1 wtedy i tylko wtedy, gdy p s 1 (mod 3).

13.    Ostatnią cyfrą dziesiętną jest 1 iub 9.

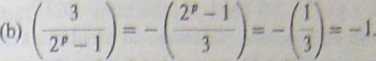
14.    Każda potęga reszty kwadratowej jest resztą kwadratową, a więc żadna nicreszta kwadratowa nie jest potęgą reszty kwadratowej. Zatem reszta kwadratowa nie może być generatorem.

15.    (a) Ponieważ p - 1 jest potęgą 2, więc rząd dowolnego elementu g jest

potęgą 2. Jeśli -1 = j = g^{p~¹⁾¹² (mod p), to ten rząd nie może być mniejszy od p - 1.

(b)

Jeśli k > 1 i p ss 2²*¹ + 1, to p s 2 (mod 5) (gdyż wykładnik tej potęgi 2

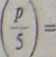
jest wielokrotnością 4). Wtedy

(c) Podobnie do (b): ponieważ wykładnik potęgi 2 nie jest podzielny przez 3, więc ta potęga dwójki przystaje do 2 lub do 4 modulo 7; stąd p = 3

lub 5 (mod 7) i = (y) = -1.

16.    (a) Zachodzi równość:

(a + ó/)^p+1 = (fl^p + b’i'Yfl + bi) - (a - bi){a + bt) = a² + b². Stwierdzenie: Jeśli (a + bi)^meF_p, to p + 1 |m. Aby dowieść tego stwierdzenia, przyjmijmy d = NWD(m, p +1). Rozumując tak samo jak w dowodzie twierdzenia 1.4.2, pokazujemy, że (a + bi)^def_p. Ale/? + 1 jest potęgą 2, więc jeśli d < p + 1, to (a + ÓQ^(P+I)/2 jest takim elementem F_p, którego kwadrat jest równy a² + b². Ale a² + b² jest nieresztą kwadratową (por. ćwiczenie 14). Zatem d = p +1 i p +1 |m. Teraz, gdy nasze stwierdzenie zostało udowodnione, przypuśćmy, że n = ri(p + 1) jest taką liczbą, że (a + bi)* - 1 (zauważmy, że ze stwierdzenia wynika, iż p + 1 |n). Wtedy (a² -I- b²)ⁿ‘ = 1, a więc p - 1 |n', gdyż a² + b² jest generatorem grupy FJ.

(b) Wykaż, że 17 i 13 są generatorami grupy Ffi.

17.    W obu przypadkach otrzymujemy oszacowanie 0(log³p). Ale zauważ, że twierdzenie 2.2.2 stosuje się tylko do przypadku, gdy liczba n jest pierwsza, podczas gdy metoda z punktu (a) ma zastosowanie ogólne, dla dowolnej nieparzystej liczby dodatniej n. Zauważ też, że czas obliczeń w punkcie (a) można zmniejszyć do 0{\og²p), stosując metodę wykorzystaną w ćwiczeniu 11 z podrozdziału 1.2.

18.    (a) Rozwiąż tę kongruencję metodą uzupełniania do pełnego kwadratu;

pokaż, że liczba rozwiązań jest równa liczbie rozwiązań kongruencji x² = D (mod p). Istnieje jedno rozwiązanie, gdy D~ 0, nie ma rozwiązań, gdy D jest nieresztą, i są dwa rozwiązania, jeśli D jest resztą kwadratową.

(b) 0, 0, 2, | 2; (c) 2, 2,1, 0,0.