Str137

™ Odpowiedni do cwicwń

7. (a) Patrz (b).

(b)    Ponieważ N - I m b (bⁿ 1 - I)/(/» - 1), gdzie licznik jest podzielny prze/, n (gdyż w jest liczbą pseudopierwszą przy podstawie b) i mianownik jest względnie pierwszy z n, więc n|A — 1. Ponieważ hⁿ 1 (mod iV) (mianowicie {b - IW - b* - 1), więc b^M~^l s 1 (mod N). Musimy także pokazać, że liczba A' jest złożona, ale to jest łatwe, jeśli skorzystamy z założenia, że n jest złożona (por. wniosek do twierdzenia 1.4.1). To, że liczba AT jest nieparzysta (niezależnie od tego, czy A jest nieparzysta czy parzysta), wynika z tego, że N możemy zapisać w postaci b* ¹ +ć"~^a + ... + &+ i.

(c)    Zacznij odpowiednio od 341, 91 lub 217 i wykorzystaj (b) do znalezienia ciągu coraz to większych liczb pscudopicrwszych. Zauważ, że warunek NWD[b — 1, n) = 1 jest zawsze spełniony dla b = 2, 3, 5.

(d)    Liczba 15 jest pseudopierwszą przy podstawie 4, ale N= (4¹⁵ — l)/3 nic jest. (Aby się o tym przekonać, zauważ, że 4 ma rząd 15 w grupie (Z/WZ)*, ale AT — 1 = 4(4*⁴ — l)/3 nie dzieli się przez 3, tym bardziej przez 15.)

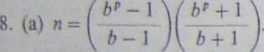
(b)    Zauważ, że liczba n jest nieparzysta (por. odpowiedź 7 (b) powyżej), a więc 2|n — 1. Następnie (n — 1 )(b² — 1) = b^z(b^z{p~^l) — 1) = 0 (mod p) i p nie dzieli (b + \)(b — 1) = b² — 1, a więcp\n — 1.

(c)    Ponieważ n jest nieparzystą liczbą złożoną, b^2p = 1 (mod ri) oraz 2p\n - 1, więc liczba n jest pseudopierwszą przy podstawie p. Ponieważ istnieje nieskończenie wiele liczb pierwszych większych niż b + 1, więc w ten sposób otrzymujemy nieskończenie wiele liczb pseudopierw-szych przy podstawie b.

9.    (a) 3²⁰⁴⁶ = 1013 (mod 2047), więc kongruenqa (1) nie jest spełniona dla

6 = 3.

(b) Gdyby były złożone, to byłyby również pseudopierwsze przy podstawie 2. Aby się o tym przekonać dla n = 2^2k + \, zauważmy, że 2²* = — 1 (mod ri) i wtedy podnosząc tę kongruencję wielokrotnie do kwadratu, otrzymamy 2""¹ = 1 (mod ri). Dla n — 2^P — 1 mamy n — 1 = 2(2^P“¹ — 1) = 0 (mod p)_t a więc 2^P = n + 1 = 1 (mod w), skąd wynika, że 2"“¹ s 1 (mod ri). Użycie kongruencji (2) dla b = 2 też nic nie da, gdyż obie strony będą równe 1, nawet jeżeli liczba jest złożona. Użycie (3) dla b — 2 też nie pomoże: dla liczb Fermata wynika to z kongruencji 2²* = — 1 (mod n), a dla liczb Mersenne’a wynika to z twierdzenia 5.1.5.

10.    Otwórz nawiasy, by pokazać, że liczba n — 1 dzieli się przez 36m, a więc przez 6m, 12m i 18 m.

12. Zakładamy, że p <q. Metoda umożliwiająca udzielenie odpowiedzi na pytania (a)-(b) jest opisana w punkcie (c).

(a) 561 = 3* 11 * 17.

(b)    1105 = 5 • 13 • 17; 2465 = 5 • 17 • 29; 10585 =» 5 • 29 - 73.

(c)    Przypuśćmy, że p < q. Ponieważ. q ~ 1 \rpq - 1 m rp - 1 (mod q- 1), więc dla pewnego a takiego, że 1 < a < r mamy rp - 1 = a(q - 1).

T akż.e p — 11 rq — 1, więc p — \\a(rq — 1)= r(aq) — a = r(a ■+■

+ rp — 1)— a = (r — \)(a + r) (mod p — 1). Zatem dla. ustalonego r i dowolnego ustalonego a z przedziału od 2 do r - 1 istnieje tylko skończenie wiele możliwych p, mianowicie liczb pierwszych takich, że p — 1 jest dzielnikiem (r — l)(a + r). Zatem każda liczba pierwsza p wyznacza jednoznacznie q, gdyż rp - 1 = a(q - V). Oczywiście nie wszystkie a i p dają liczbę Carmichaela (np. liczba a może nie dzielić rp — 1).

13. Każda liczba Carmichaela nie wymieniona w ćwiczeniu 12 (a)-(b) musi być iloczynem co najmniej trzech różnych liczb pierwszych, nie mniejszych niż 7.

■L « = 21, 6 = 8.

___l. (a) Z ćwiczenia l(d) wynika, że musimy sprawdzić tylko te liczby 6, dla

sisiMls

których

(mod    2 p — 1).    Ponieważ

n — 1 s p — 1 (mod 2p — 2), więc 6⁰¹ 1)12 = 6^ ^l)f2 (mod p) i (mod 2p — 1), to znaczy 6^lB“^11/2 =    ¹⁾¹² (mod n). Teraz

= 6^ ^1W2 (mod p).

I

1)1*

a więc warunek (2) zachodzi wtedy i tylko wtedy, gdy bP

(mod 2p — 1). Jest tak dla dokładnie połowy wszystkich 6, dla których b^p~¹ = 1 (mod 2p — 1) (ponieważ w grupie (Z/(2p — 1)Z)* taki ele-

>    P — 1

ment 6 musi byc taką potęgą g^J generatora g, że —-— j = 0 (mod 4)

dla

(7-

= 1 oraz

7 = 2 (mod 4) dla

i

= -1)-

(b) n — p(2p — 1), gdzie p = 3 (mod 4) (z twierdzenia 5.1.5).

17. Oblicz resztę z dzielenia n przez 72m: n = 36m² 4- 36m 4- 1. Zatem

— = 18m(m 4* 1) (mod 36m). Jeśli liczba m jest nieparzysta, to zawsze mamy 6^ln-1)/2 = 1 (mod n) (ponieważ p — l|36m dla wszystkich p\n), a więc (2) zachodzi wtedy i tylko wtedy, gdy = l, tzn. w 50% przypadków. Jeśli liczba m jest parzysta, to nadal mamy b⁽ⁿ~^i)l2 = 1 (mod 6m 4- 1)

\ 12m 4-1 )

n

12m 4-1

12m 4- 1). Zatem w tym przypadku (2) zachodzi wtedy i tylko wtedy, gdy

i (mod 18m 4- 1), podczas gdy P

»- l)/2 =

(mod