ullman088 (2)

1X2 3. RELACYJNY MODEL DANYCH

Niech / oznacza pewną krotkę R. Zapiszmy jajako (a, b, c), gdzie a, b, c oznaczają odpowiednie składowe / dla atrybutów Z?, C. W wyniku rzutowania / na schemat {/f, /?} otrzymujemy krotkę (>a, b), a na schemat {B, C} krotkę (b, c).

Jeśli wartości składowej B w schematach {A, B) oraz {B, C) są równe, to możemy wykonać złączenia odpowiednich krotek. W zasadzie (a, b) zawsze można połączyć z (b, c) i w ten sposób otrzymać początkową krotkę t = (a, b> c). Nie jest to zależne od wyboru krotki I, a więc w każdym przypadku wykonalne.

Ale wykonalność odtworzenia krotek sprzed dekompozycji nie świadczy jeszcze o wdemym reprezentowaniu relacji R w schematach powstałych po dekompozycji. Co może się zdarzyć na przykład z dwiema krotkami R: / *= («. b, c) oraz v = (d, b, <?)? Po zrzutowaniu R na {A. B) otrzymamy u = (a, b), a gdy zrzutujemy v na {B, C}, otrzymamy w-(ó, <?); przedstawiono to na rys. 3.37.

w

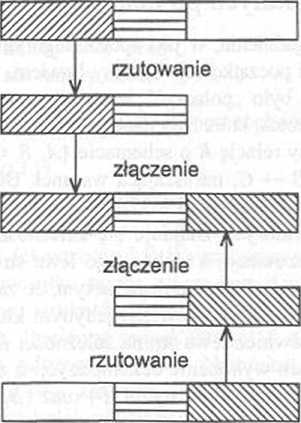
RYSUNEK 3.37

/.łączenie dwóch krotek ze zrzutowanych relacji

Można połączyć krotki u i w> ponieważ mają te same wartości składowej B, w wyniku otrzymamy krotkę * = (a, b, e). Czy w takim razie x jest krotką fałszywą? Przecież (a, b, e) nie ma w schemacie R.

Jeśli przyjmiemy, że w relacji R zachodzi zależność funkcyjna B —► C, to odpow iedź brzmi „nie”. Znaczenie tej zależności polega przecież na tym. że jeśli dwie krotki R są zgodne dla atrybutu B, to muszą być zgodne również dla atrybutu C. Ponieważ krotki t oraz v są zgodne dla składowej B (w obu występuje ta sama wartość b), to muszą mieć również takie same wartości dla składowej C. A to znaczy, że c = e, a więc dwie wartości, które można podejrzewać o to, że są różne, w istocie rzeczy są takie same. A więc (a, b, e) je to ta sama krotka co (a, b, c), to znaczy x = t.

Ponieważ t należy do R, zatem krotka x też należy do R. Mówiąc inacze o ile tylko zachodzi zależność B —► C, to połączenie dwóch krotek powstałyc z rzutowania nie może stanowić krotki fałszywej. Każda krotka utworzoi w wyniku połączenia na pewno jest krotką z R.

Uzasadnienie to obowiązuje również dla przypadku ogólnego. Zakłada śmy, że A, B, C są pojedynczymi atrybutami, ale rozumowanie będzicn prowadzić w ten sam sposób, jeśli będą one zbiorami atrybutów. A zate niech dana będzie zależność, która nie spełnia warunku BCNF; zbiór atryb tów B niech występuje po lewej stronic tej zależności, a zbiór C po prawej, 2 nie po lewej, a zbiór A nie występuje ani po prawej, ani po lewej stronic ? leżności. Wówczas:

• Jeśli wykonamy dekompozycję relacji metodą opisaną w p. 3.7.4, pierwotną relację można dokładnie odtworzyć przez wykonał wszystkich możliwych połączeń krotek nowych relacji.

Jeśli natomiast wykonanie dekompozycji nie jest związane ze stosowani* zależności funkcyjnych, to odtworzenie pierwotnej relacji może być nicv konalnc. Poniżej przedstawiamy przykład takiej sytuacji.

PR/.YKLAD 3.41

Załóżmy, że relacja R została zdefiniowana tak samo jak powyżej, jako {A. C}, ale nie zachodzi w niej zależność B —> C. Wówczas w R mogą wystę wać następujące krotki:

A	B	c
1	2	3
4	2	5

W wyniku rzutowania R odpowiednio na schematy {A, B} oraz C} otrzymamy

oraz

A	B
1	2
4	2
B	c
2	3
2	5