wykad1039

x(t)

Kwantyzacja sygnału - r. 4, [1] (r. 9.3.1 [2])

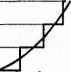
^a x(t) - sygnał

Ta~

^(t)-sygnał ^kwantowany mierzony

t

Błąd kwantowania: e(t) = x(t) - x(t)

Błąd kwantowania n-tej próbki:

- —<e(nT)< —

2 2

Próbka n-ta sygnału z przetw. A/C: x(nT) = x(nT) + e(nT)

Błąd kwantyzacji (r. 4.2, [1]):

Z dobrym przybliżeniem można przyjąć, że błąd e jest sygnałem losowym o równomiernym rozkł. prawd., tzn. o gęstości prawdopodobieństwa p = 1/ A:

	4 1/A	P
A		A

2 2

Jakość kwantyzacji określa się współczynnikiem SNR (signal-to-noise-ratio):

Zatem

X

SNR =

sk

A² /12

(4.2)

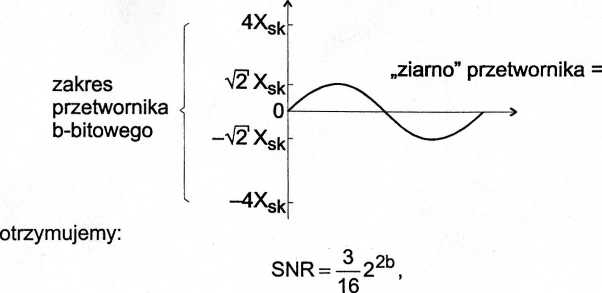
Np. dla sinusoidy z pełnym wy > r V2Xsk zakres przetwornika i o b-bitowego ^1 -^xsk otrzymujemy: SNR = ^2^2b, a	korzystaniem zakresu przetwornika: 2V2’Xsk „ziarno” przetwornika =
	w decybelach: SNRdB = 10log^2^2b , czyli:
SNRdB =6,02 -b +1,76 [dB] Wzrost liczby bitów przetwornika A/C o 1 bit poprawia dynamikę przetwarzania analogowo-cyfrowego o 6 dB.

[2], (9.15)

snr ^{moc sygnału}

moc szumu kwantowania

moc sygnału = X²k,

moc szumu = wartość oczekiwana kwadratu błędu e o rozkładzie równ. =

o A/2

= E[e²]_:

A/2

J P

-A/2

e² = —

1 e"

A 3

-A/2

A^

12

przetwornika zapobiegającym jego

Dla sinusoidy z nadmiarowym zakresem przesterowaniu:

8X_sk

2^b

(4.4)

a w decybelach:

SNR_dB =6,02-b-7,3 [dB] (4.5)