Untitled Scanned 16 (9)

Możemy tego dokonać w dwojaki sposób: albo obliczyć reakcje i w dowolnym przekroju określić szukane siły wewnętrzne, albo korzystając ze wzoru (9.5) wyznaczyć poszukiwane wielkości jako sumę iloczynów sił powodowanych jednostkowymi obciążeniami pomnożonych przez rzeczywiste wartości niewiadomych sił od obciążeń zewnętrznych. Na przykład M=M₁Xi + M₁X₂ + M_p. Wykresy MtXi oraz M₂X₂ pokazano na rys. 13.13j, k, a M_p na rys. 13.13e, f. Sumując te wykresy otrzymamy wykres momentów M dla układu rzeczywistego od danych obciążeń (rys. 13.131).

Siły poprzeczne obliczymy wyznaczając kolejno reakcje poszczególnych prętów, traktowanych jako podparte przegubowo, obciążone momentami przy podporach i danym obciążeniem zewnętrznym. Obliczmy więc siły poprzeczne dla poszczególnych prętów ramy.

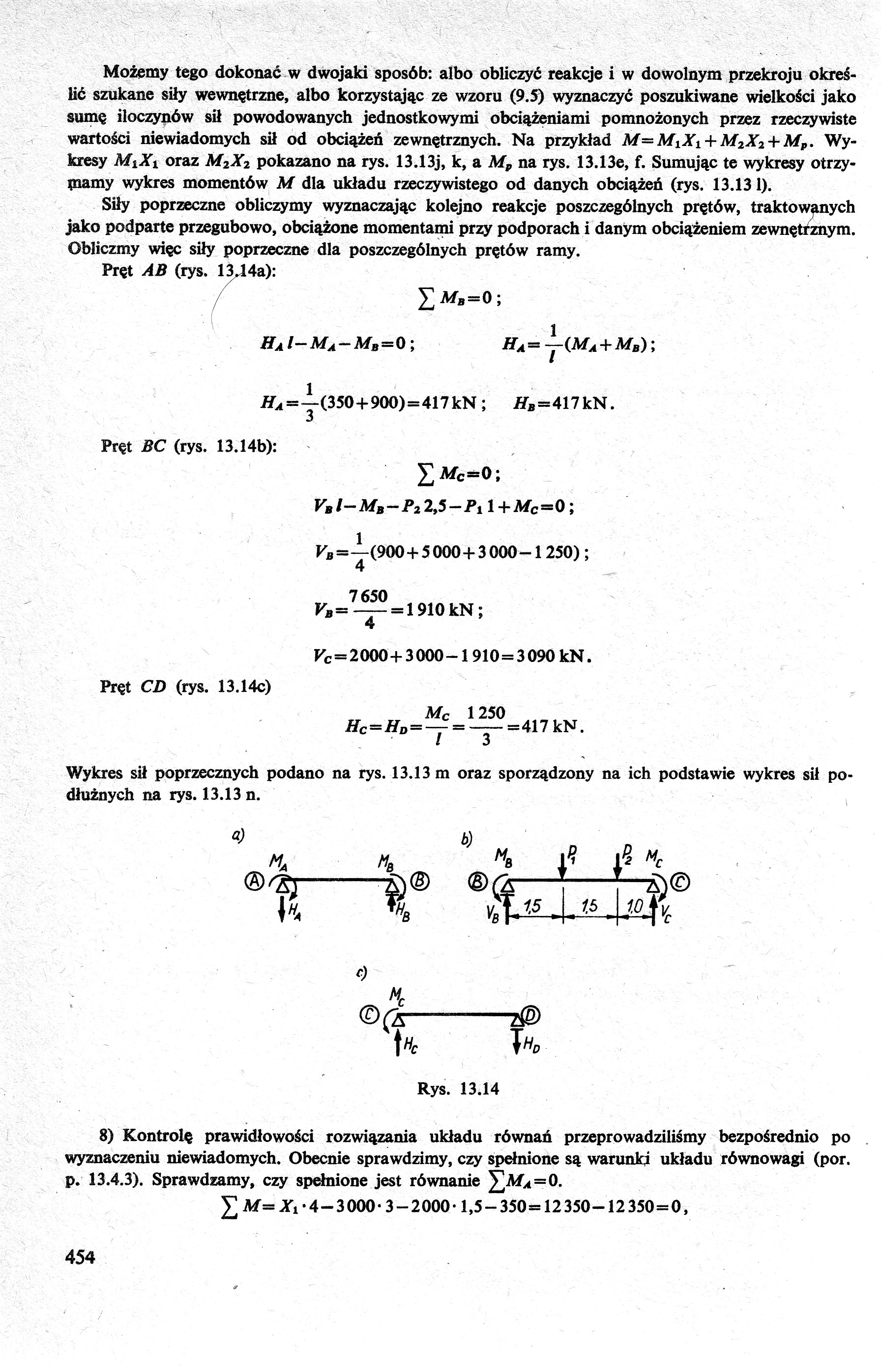
Pręt AB (rys. 1344a):

E^»=o;

H_Al-M_A-M_B=0;

#*=—(350+900)=417kN; fl_B=417kN.

Pręt BC (rys. 13.14b):

£Mc=0;

/-Af„ - P₂ 2,5 - Pj 1 + M_c=0 ;

V_B=—(900 + 5 000 + 3 000 -1250) ; 4

7650

V_B=-= 1910 kN;

4

Pręt CD (rys. 13.14c)

Kc = 2000 + 3000—1 910 = 3090 kN. M_c 1250

#_c = tf_D = _ = —_ =417 kN.

Wykres sił poprzecznych podano na rys. 13.13 m oraz sporządzony na ich podstawie wykres sił podłużnych na rys. 13.13 n.

^Mc

®(ŹT--Z®

t H_c    Jh_d

Rys. 13.14

8) Kontrolę prawidłowości rozwiązania układu równań przeprowadziliśmy bezpośrednio po wyznaczeniu niewiadomych. Obecnie sprawdzimy, czy spełnione są warunki układu równowagi (por. p. 13.4.3). Sprawdzamy, czy spełnione jest równanie ^Mi=0.

£ M=4Ti-4-3000-3-2000-1,5-350=12350-12 350=0,

454