Untitled Scanned 19

- 38 -

zawierał wszystkie składniki jedności. Niezbędne do tego inw plikanty zaznaczono na rys.2.5 symbolami    Ostatecznie na

podstawie rys.2.5 otrzymuje się

y -    + 5₃x₄ + x₁x₂x₃

Analogicznie przebiega proces minimalizacji kanonicznej postaci koniunkcyjnej. Przykład minimalizacji funkcji

=»    0,1,2,5,8,9,10,13* 14,15 ⁿ

» 3r 3,4,6,7,11,12

pokazano na rys.2.6. a)

I	I	iii	il
D3 -X1*X2*^• 7^	0 0 11	0 1 oov	0 1 - 0 -
°4 ^= X1 * *2 * ^x3 * *4	0 10 0	0 0 1 1 V	- 1 0 0 -
°6 =*l**2**3*^x4	0 110	0 1 1 0 V	0-11 •
Dy sXj*X2*x"3**4	0 111	1 1 0 0 V	- 0 1 1 *
W *2* *3 **4	10 11	0 1 T 1 V	0 1 1 - *
Dj2»7i ♦x’2*^j<3*^,<4	110 0	1 0 1 1 V

b)

Implicenty	0 0 11	c 0100	zynnlki 011 0	zera 0111	10 11	1 100
0 1-0		V	V
-1 0 0 *		V				V
0-11	V			V
-011*	V				V .
0 1 1 - *			V	V

y-(X₂*x₃    ł*Cx_t *x₂* x₃)

Rys.2.6. Przykład minimalizacji kanonicznej postaci koniunkcyjnej metodą Quine*a-McCluskeya: a) przebieg procesu sklejania; b) tablica impli-

centów

Metoda Quine*a-licCluskeya nadaje się do minimalizacji funkcji o dowolnej liczbie argumentów.

2.4. SYNTEZA FUNKCJI NIE W PEŁNI OKREŚLONYCH

W praktyce, przy formułowaniu założeń działania układu przełączającego niekiedy stwierdza się, że:

-    nie Jeat możliwe lub celowo wyklucza się wystąpienie niektórych kombinacji wartości sygnałów wejściowych,

-    dla niektórych kombinacji wertości sygnałów wejściowych wartość sygnału wyjściowego nie jest istotna - można ją przyjąć dowolnie.

Stany argumentów odpowiadające wymienionym przypadkom nazywają się obojętnymi. W ceiu odróżnienia ich od stanów określonych,wartość funkcji w stanach obojętnych zaznacza się w tablicach wartości za pomocą kreski. VS zapisach symbolicznych numery stanów obojętnych podaje się w

O)    b)

\*3*A    \3\

00

01

11

f)

1	1	1	1
1	-	if"	'0'i
	-	1-V —	(Cl
1 V®.	1	1

*l*2\nnni ¹¹ 10    *1*2

00

01

11

10

(1				li
1		y	-	0
0		-	-	0
0		i_	1	0

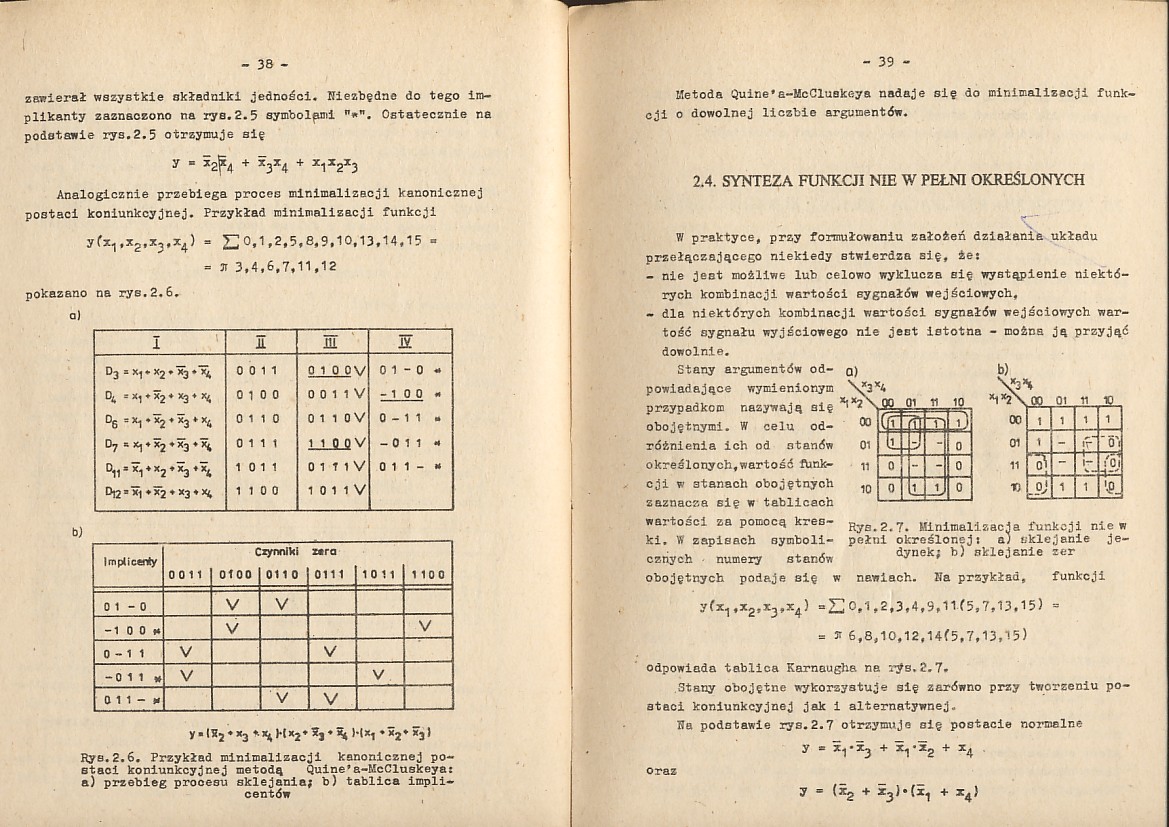
Rys.2.7. Minimalizacja funkcji nie w pełni określonej:    a) sklejanie je

dynek; b) sklejanie zer

nawiach. Na przykład, funkcji

y(*1 **2*^x3,^x4) = 2⁰*¹*².3,4,9,11(5,7,13.15) =

= 3: 6,8,10,12,14(5,7,13,15)

odpowiada tablica Karnaugha na rys.2.7.

3tany obojętne wykorzystuje się zarówno przy tworzeniu postaci koniunkcyjnej jak i alternatywnej.

Na podstawie rys.2.7 otrzymuje oię postacie normalne y « 5^X3 + *Xg + x₄ .

oraz

y = (ig +    + x₄)