Image28 (20)

54
e) as =
b2ct
b2r
=
bc (h2t2 + 2)
<pr (p2 + 2)
t2Vl +
O p =
T (1 + <p2)3/2
<P (2 + <p2)
i t
v 1-19. a. Przyjmując warunki początkowe
x(0) = x(0)
0
i
y(0) =
otrzymujemy
r cos<p = fet2,
y = r swcp = ct
Stąd, po prostych przekształceniach, mamy:
i2 \Jb1 + c2,
9 = arctg
b. Z definicji prędkości
vr — r = 2t <jb2 + c2,
*>«. = r<p = 0,
skąd
v — 21 y/b2 -f c2.
Z definicji przyspieszenia
ar = r — rep2 = 2 yjb2 -f c2, av — rep + 2 rep = O,
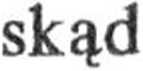
a = 2 sjb2 -f c2.
1.20. Szukamy równania toru w biegunowym układzie współrzędnych (rys. 14).
Z warunków zadania wynika, że w przyjętym układzie odniesienia
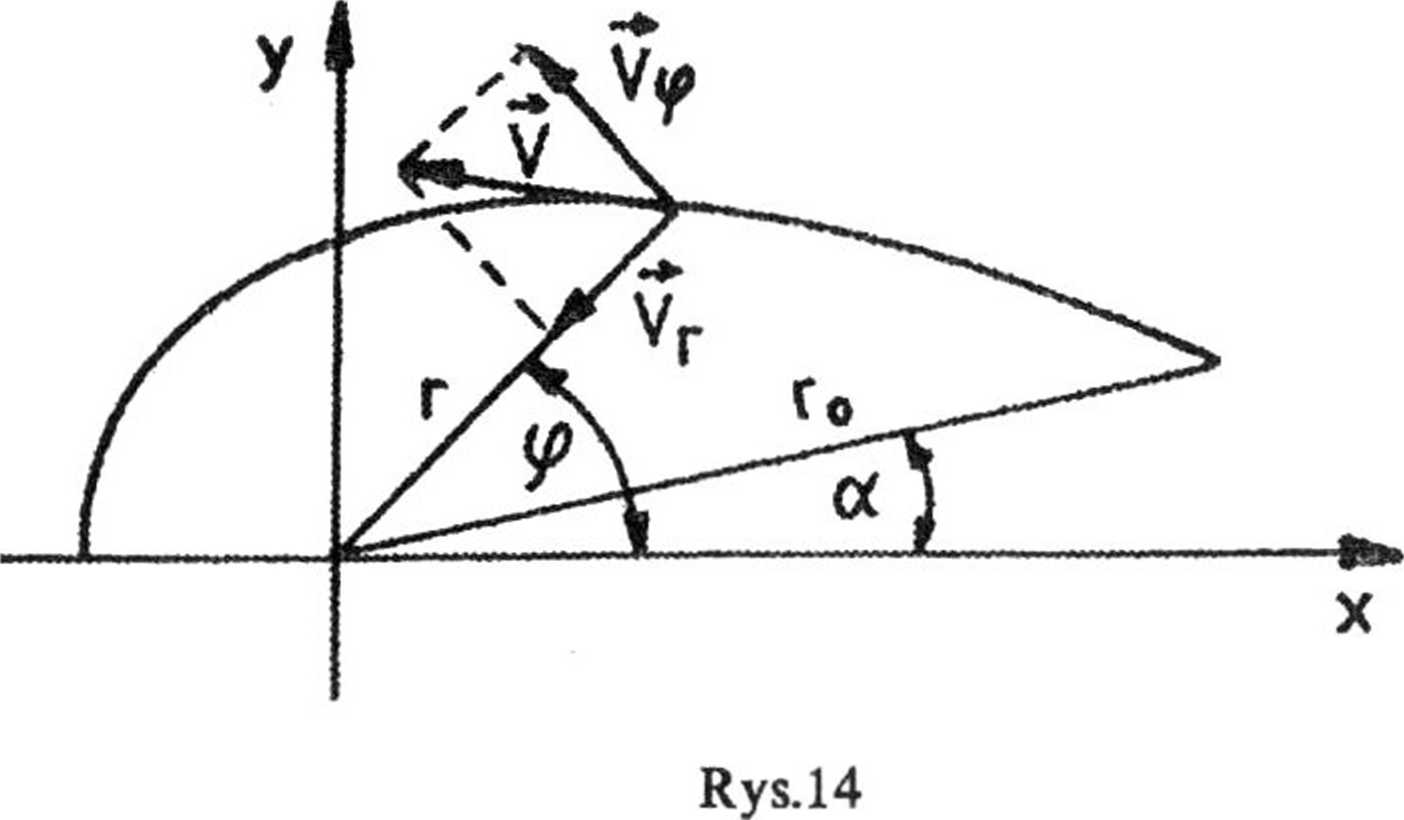
vr = u,
gdzie u jest prędkością dźwięku. Ponieważ
Vv = y/v2 - V,1 = yfj2 - u2,
to
u* = const,
a stosunek — ma wartość stałą

Korzystając z tego, iż = rep oraz vr = — r, otrzymujemy równanie różniczkowe:
rep _ y/v2 — u2
a- ,
r u
które

ożna zapisać w innej postaci
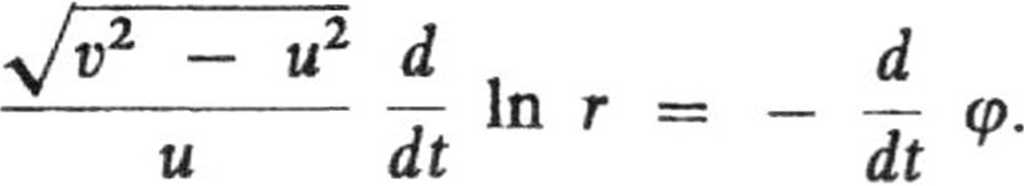
Wyszukiwarka
Podobne podstrony:
47221 Image28 54 e) as = b2ct b2r/i + /?2 t2 ^rry Cl = bc (b212 + 2)V7! + bY? (pr ( &nbs
Image25 (30) 1 54 Rozwiązania zadań ze zbioru "MENDLA" P1 =P2 = P Temperatury obu gazów ró
skanuj0016 (54) -3- 9.2 Stwierdzenie, że trójkąt ABC jest równoboczny, oznaczenie długości jego b
slide0603 image294 r«mlKH t»irOU as u«j Qr»n<vr □*% □ u^grtł □
HWScan00059 a4 aa •54 aS ta •J* «: SrHI • ?- £ E ii a V wili; •*• y, ■
100c81 Kopia wymunw R
DSC00320 (20) 54 54 Zaliczenie z escmet I . Uzupełnić przekrój otaszczyzna wicie ścicnu ■ 1
więcej podobnych podstron