Image25 (30)

1

54

Rozwiązania zadań ze zbioru "MENDLA"

P1 =P2 = P

Temperatury obu gazów również są identyczne: Ti = T₂ = T

Z równania Clapeyrona dla wodoru otrzymamy:

p-Vi mi

T

p • Vi = V1 =

R AT

mi • R • T

Pi

mi • R • T

/: p

P1 • P

Podobnie dla azotu otrzymujemy: rri2 • R • T

V₂ =

H2 • p

Teraz stosunek objętości wodoru Vi do objętości naczynia możemy zapisać w postaci:

Vi Vi V

Vi + V₂

Do prawej strony równania podstawiamy wyznaczone Vi i V₂₎ mi • R • T

Yi

v

stąd

mi • R • T m₂ • R • T

+

P1 • P P2 • P Przekształcamy otrzymaną zależność: mi • R • T Vi V

m • p

V1

V

mi • R • T • [12 + m₂ • R • T • pi P1 • H2 • p

mi • R • T _pi • P2 • p

|A1 • P Ostatecznie mamy:

Vi__mi • p₂

V “

R • T • (mi • ^2 + m₂ • m)

mi • p₂ + m₂ • pi

SL

V

3g ■ 28

mol

³9'²C/^ł18-9'²™/

Yi

v

84

jL

mol

84

A

mol

84

A₊₃₆A ₁₂₀A

= 0,7

mol mol mol Odp.: Wodór zajmuje 0,7 objętości cylindra.

t

Rozwiązania zadań ze zbioru "MENDLA

55

Zadanie 572 str.114

Dane:    Szukane:

_tl = 47°C, ale Ti = 273K+ 47/<= 320K    ^h = ?

I _s 76 cm = 0,0760 m

t3 = - 33°C, więc    T₂ = 273K- 33K = 240K

p_A = 1000hPa =» 760 mHg- co odpowiada ciśnieniu

hydrostatycznemu rtęci: pa = p g I

₀ = 13600-— - gęstość rtęci

^K nr

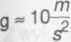
t₂

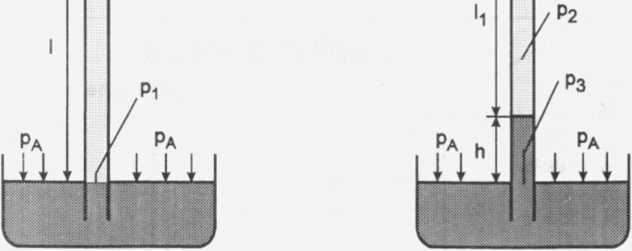
Z własności naczyń połączonych wiadomo,że ciśnienie cieczy na tym samym poziomie w różnych ramionach jest takie samo, więc:

< D. II CL	P3 = pa, lecz	P3 = p2 + h • p • g
stąd	P2 + h • p • g = pA
ale pi = p • g • I	cn Cl _C 1 < CL II a	gdzie pa = p • g • I
więc	cn CL SI 1 cn CL II CM CL
p2 = p • g • (I - h) Z równania gazu doskonałego dla obu stanów gazu otrzymamy:
Pi ■ Vi p2 ■ V2 Ti " T2 ’	ale Vi = S • I	i V2 = S • (I - h)

Po podstawieniu:

S - pole przekroju rurki

/: p • g • S

p • g • I • S • I _ p • g • (I - h) • S • (I - h) Ti    T₂

/•t₂

j! _ (I ~ h)² Ti T₂