img345 (4)

Rozwiązanie. Na podstawie informacji zawartych w tabl. 147 ustalamy stopę przybyć w ten sposób, że stosujemy odwrotność przeciętnego czasu dzielącego dwóch kolejnych klientów (54:36 = 1,5 min), czyli X = 2/3 osoby na min. Podobnie ustalamy przeciętny czas obsługi 60 min: 36 = 5/3 min na

osobę

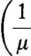
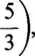
a zatem p = 3/5 osób na min.

Wykorzystując wartości obu parametrów, ustalamy trzeci parametr:

P

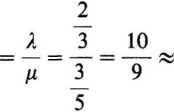
1,1.

Porównanie wartości X oraz p wskazuje, że zachodzi między nimi nierówność X>p, czyli że stopa przybyć przewyższa stopę obsługi. Dodając do tego wartość parametru p>l, należy stwierdzić, że badany układ jest niestabilny, a prawdopodobieństwo długiej kolejki się zwiększa. Tak więc osiągnięcie stanu równowagi jest możliwe tylko w przypadku zmiany warunków działania. Należy zatem sugerować kierownictwu poczty dwa możliwe rodzaje działania:

a)    usprawnić obsługę klientów (skrócić przeciętny czas obsługi),

b)    zainstalować dodatkowe stanowisko obsługi.

Biorąc zaś pod uwagę fakt, że według opinii kierownictwa poczty obsługa okienka ds. wpłat i wypłat gotówkowych jest bardzo sprawna, pozostaje drugie rozwiązanie - uruchomienie jednego dodatkowego stanowiska w godzinach: 14.00 - 18.00.

Przykład 28. W sklepie samoobsługowym funkcjonuje jedno stanowisko kasowe. Obserwacje poczynione na przybyciach klientów oraz pracy kasjera dały następujące wyniki: przeciętnie co 10 min przybywa 25 kupujących oraz w ciągu 10 min inkasujący gotówkę kasjer zdąża obsłużyć średnio 20 klientów. Po pewnym czasie właściciel postanowił zainstalować nowy, lepszy rejestrator kasowy (z fotokomórką), co pozwala kasjerowi w ciągu 10 min obsłużyć przeciętnie 31,25 osób.

1.    Zanalizować stan obsługi kasowej w sklepie przed wprowadzeniem i po wprowadzeniu nowych rejestratorów, posługując się analizą parametrów X, p oraz p.

2.    Udzielić odpowiedzi na dodatkowe pytania właściciela sklepu:

-    Jak duża jest przeciętna liczba klientów oczekujących w kolejce?

-    Jakie jest prawdopodobieństwo, że w kolejce będzie stało więcej niż 5 osób?

-    Jakie jest prawdopodobieństwo, że kupujący będzie stał w kolejce oczekując na obsługę dłużej niż: a) 1 min, b) 2 min?

Zakłada się, że przybycia klientów odbywają się w sposób losowy, rozkład przybyć jest rozkładem Poissona, a czasy ich obsługi tworzą rozkład wykładniczy.

Rozwiązanie. Przystępując do analizy sytuacji przed wprowadzeniem

usprawnień, należy wyznaczyć wartości parametrów X, p oraz p:

25

A = — = 2,5 osoby/mm,

20 , , , p =—=2,0 osoby/mm,

P

X_l$

p 2,0

= 1,25.

Otrzymane parametry wskazują, że układ obsługi jest wysoce niestabilny: X > p oraz p > 1. Prawdopodobieństwo długiej kolejki rośnie, co sugeruje, że w układzie należy wprowadzić zmiany.

Wprowadzenie usprawnienia w postaci zakupu nowego, szybszego rejestratora wychodzi naprzeciw oczekiwanym zmianom. Należy zatem powtórnie dokonać analizy podstawowych parametrów charakteryzujących układ. Zakłada się przy tym, że stopa przybyć kształtuje się na nie zmienionym poziomie.

Po wprowadzonych zmianach parametry opisujące układ przyjmują następujące wartości:

A = 2,5 osoby/min,

p =

31,25

10

= 3,125 osoby/min,

= 0,8.

2,5

3,125

Ponieważ X < p oraz p < 1, możemy uznać, iż w badanym układzie sytuacja się poprawiła. Prawdopodobieństwo długich kolejek maleje, a układ jest w miarę stabilny. A oto odpowiedzi na pytania właściciela sklepu:

Przeciętną liczbę klientów oczekujących na obsługę (Q) otrzymuje się wykorzystując następujący wzór:

(0,8)²

1-0,8

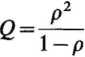
= 3,2,

zatem w sklepie tym po wprowadzonej zmianie średnio 3,2 osoby oczekuje w kolejce na obsługę. Jest to stosunkowo niewielka liczba, co oznacza korzystną sytuację dla klienta.

Prawdopodobieństwo tego, że w kolejce będzie czekało więcej niż n₀ osób, określa wzór:

P(ⁿ>n₀) = Pⁿ°⁺¹ ■

Wobec tego

p (n > 5) = (0,8)^{5 +1} w 0,262144 tu 0,26.

147