LS Miern energ (dla Student) 13

OPRACOWANIE WYNIKÓW POMIARÓW

Szacowanie niepewności pomiarów i metody obliczania niepewności pomiarowych Ocena niepewności przypadkowych

Wielokrotne niezależne pow tarzanie tego samego pomiaru fizycznego pozwala otrzymać serię wyników x_lt x₂, x₃ .... x„ (gdzie n - oznacza liczbę wykonanych pomiarów).

Rzeczywista wartość wielkości fizycznej nie jest znana, ale najbardziej zbliżona do niej jest średnia arytmetyczna otrzymanych wyników x , obliczana ze wzoru:

1 *

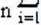
Wyniki pomiarów układają się wokół wartości średniej arytmetycznej. Przy bardzo dużej liczbie pomiarów' («-»co) rozkład ten może być opisany funkcją, zwaną rozkładem Gaussa:

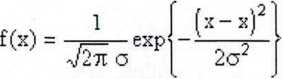
gdzie: f(x) - gęstość prawdopodobieństwa,

o - odchylenie standardowe, będące miarą niepewności pojedynczego wyniku pomiaru:

Miarą niepewności średniej arytmetycznej x jest jej niepewność standardowa:

a

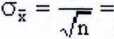
n(n-l)

1

Rozkład prawdopodobieństwa Gaussa daje możliwość obliczenia prawdopodobieństwa, że dowolny wynik pomiaru znajduje się w zadanym przedziale wartości x, tj.:

400

/ \

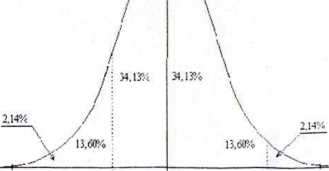
3a    2c c    x    o 2o Ja

w przedziale:

(x-o, x + O) mieści się 68,27 % wyników, (x - 2ct, x + 2ct) mieści się 95,45 % wyników, (x - 3ct, x + 3a) mieści się 99,73 % wyników.

Krzywa Gaussa rozkładu niepewności przypadkowych (wartości liczbowe określają procentowe prawdopodobieństwa pojaw ienia się wyniku pomiaru w wyznaczonych przedziałach)

OPRACOWANIE WYNIKÓW POMIARÓW

Szacowanie niepewności pomiarów i metody obliczania niepewności pomiarowych Przykład: ocena niepewności przypadkowych

Pomiar grubości płytki za pomocą mikrometru (dokonany n = 10 razy) dał wyniki:

*	cl [liiIIII	A-d	(d - d )'-
1	8,07	-0,068	4624-10’^6
2	8,10	-0,038	1444 10 ^6
3	8,12	-0,018	324 10^6
4	8,17	+0,032	1024 10 ^6
5	8,14	+0,002	4-10*
6	8,16	+0,022	484-10*
7	8,17	+0,032	1024-10*
8	8,13	-0,008	64-10*
9	8,14	+0,002	4 10*
10	8,18	+0,042	1764-10*

= 81,38

!-l

Wartość średnia d :

1 ¹¹

d — x = — V dj = 8,138 mm

ⁿ i=i

= 10760-10'⁶

!-l

Odchylenie standardowe pojedynczego pomiaru:

1 i “    _ 2

cr= J—jS(^di“ ^d) = 0,0346 mm

Niepewność standardowa średniej arytmetycznej:

Oj =-Ę== 0,0109 mm Vn

Przedstawiony przykład pokazuje, że wykonując serię pomiarów wielkości fizycznej:

•    obliczamy średnią arytmetyczną x, która jest najbardziej zbliżona do wartości rzeczywistej,

•    jako niepewność oceny ii przyjmujemy wartość odchylenia standardowego średniej arytmetycznej C_s, która jest nazywana niepewnością standardową,

•    wynik końcowy zapisujemy w postaci: x ±

W podanym przykładzie:

d = d ± 05

po zaokrągleniu: d = (8,14 i 0,01) min