Misiak8

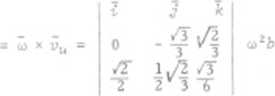
Gun

a_un = w²b(- 2^ +    3 *    *)

Przyspieszenie punktu w ruchu względnym wynoBi

ciy « ai

Przyspieszenie Coriolisa obliczamy ze wzoru (3.5)

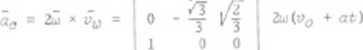
a_c = 2<x (Uj, ♦ aż)?

Wektor bezwzględnego przyspieszenia punktu /-/jest równy

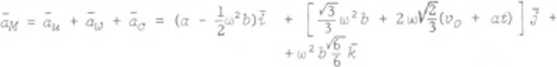
Przykład 3.5. Dany jest ostrosłup o podstawie kwadratowej obracający się dookoła krawędzi AZ (rys. 3.5) z prędkością kątową u> =

= 3t s^_l . Pur.kt « porusza się po obwodzie okręgu wpisanego w płaszczyznę podstawy ze stała prędkością V. Znaleźć prędkość bezwzględny i przyspieszenie bezwzględne tego punktu, gdy będzie się on znajdował w położeniach F i G, jeżeli wiadomo, że krawędź podstawy i wysokość ostrosłupa są równe l.

Rozwiązanie

Prostokątny ruchomy układ współrzędnych przyjęto na osi obrotu w punkcie A. Wektory prędkości kątowej <3 i przyspieszenia kątowego C leżą na osi obrotu i wynoszą:

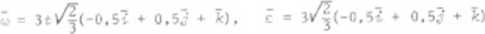
Obliczamy prędkość i przyspieszenie bezwzględne punktu M, gdy znajdzie się on w punkcie F. Położenie tego punktu opisuje promień--wektor

~r_F = 0,5£(-ę + 2j)

Prędkość punktu w ruchu unoszenia jest równa

I i J * I

o_u a w x rp = I -0,5 0,5    1 | 3ij V ^ 0,51

I -1    2    0 |

V_u = 3tj/Ęn-ł - 0,5? - 0.25*)

Prędkość punktu w ruchu względnym wyrosi

Py = -Vi

78