P3200164

256 4. Analiza skupień

zbędne, aby poprawnie wyznaczać mierniki odległości taksonomicznej. Ma ono do spełnienia następujące cele (zob. Mynarski, 1992; Chojnacki i Czyż, 1973):

1)    doprowadzenie różnoimiennych cech do porównywalności,

2)    ujednolicenie charakteru zmiennych⁶⁸,

3)    wyeliminowanie z obliczeń wartości ujemnych (jeśli takie występują),

4)    ustabilizowanie zmienności.

Istnieje wiele różnych procedur normalizacyjnych. Można je wszystkie zdefiniować ogólnym wzorem (zob. Grabiński, 1991, Domański i inni, 1998)

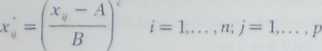
gdzie A, B i c są parametrami, które przyjmują różne wartości w zależności od sposobu normalizacji.

Wśród procedur normalizujących szczególne miejsce zajmuje standaryzacja. Przyjmijmy, że jej istota polega na wyrażeniu wartości zmiennej w jednostkach odchylenia standardowego. Najpowszechniejszą formą standaryzacji jest transformacja według wzoru (1.9)

x, — x,

v i .    ,    >i

²a =—;- t = 1,1.....p

⁵i

prowadząca do wyrażenia wartości zmiennej w jednostkach odchylenia standardowego jej odchylenia od średniej. Ten sposób standaryzacji pozwala porównywać wartości różnoimiennych zmiennych ze względu na ich względne położenie w rozkładzie. Zmienne standaryzowane są bowiem wielkościami niemianowa-nymi o średniej równej zero (z. = 0) i wariancji równej jeden (s(z.) = 1). Jest to procedura „najpełniejsza” z punktu widzenia celów transformacji, a przez to najczęściej stosowana.

Innym sposobem standaryzacji jest wyrażenie zmiennej pierwotnej w jednostkach odchylenia standardowego

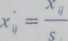
Tak utworzona nowa zmienna jest niemianowana, o średniej x] = x M. i wariancji równej 1. Stabilizuje ona zatem wariancję, lecz nie relatywizuje położenia rozkładu zmiennej.

Standaryzacja jest najczęstszą formą normalizacji. Stosuje się ją w odniesieniu do pomiarów w skali interwałowej niemal bezdyskusyjnie, zmienna po zmiennej.

Ten cel jest ważny w porządkowaniu liniowym metodą wzorca, zob. rozdział 5

4.5. Procedury normalizacji zmiennych

25

Niemniej jednak standaryzacja według wzoru (4.83) powoduje zmianę relacji wartości zmiennych

X. — X X.

jc₂ — jr s

■-- 9* —

X, — X X ,

gdzie x, i x₂ są dwiema różnymi wartościami tej samej zmiennej X. zaś s jej odchyleniem standardowym, i jest to efekt przcskalowania wartości zmiennej w drodze ich centrowania: x ~~x .

Everitt (1993) zwraca uwagę, że może to doprowadzić do pewnej niekorzyst nej sytuacji, polegającej na zniekształceniu różnic między grupami ze względu na zmienne, które są w istocie dobrymi dyskryminatorami Problem polega na tym że rozrzut punktów według wyjściowych wartości zmiennych który ujawnia istnienie grup, może po standaryzacji te różnice zacierać Nic będą więc one dosta tecznie uwzględnione w miarach odległości, a w konsekwencji rozdzielenie grup może się okazać co najmniej utrudnione Waga problemu polega więc na zatarciu nie tylko bezwzględnych, ale i względnych różnic Everitt zarzuca także sianda ryzacji każdej cechy odrębnie to, że ignoruje możliwe korelacje między zmień nymi. To stwierdzenie pozostaje jednak w sprzeczności z faktem, że standaryzacja nie zmienia współczynników korelacji, co najwyżej stawia znak rownosci między współczynnikiem korelacji a kowariancją, która i lak ma ograniczone znaczenie w analizie skupień.

Nie bez wpływu na relacje między wartościami zmiennej jest też drugi sposób standaryzacji, według wzoru (4.84). Normalizacja poprzez dzielenie przez odchylenie standardowe (tj. stałą s.) zachowuje co prawda względne znaczenie poszczególnych wartości

X, / S    X

—    (4.86)

ale zniekształca relacje w wymiarze bezwzględnym, zmniejszając różnice między wartościami s-krotnie. Z tego punktu widzenia należałoby wyżej ocenić drugi sposób standaryzacji, co jeszcze nie przesądza o ich rzeczywistych zastosowaniach Drugim sposobem normalizacji zmiennych jest przekształcenie ilorazowe, postaci

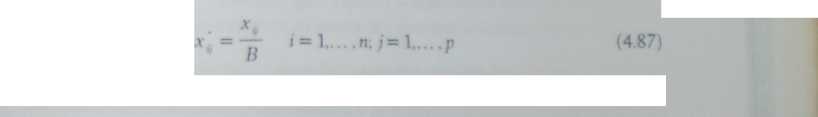
gdzie B, zwane podstawą normalizacji, może być określone różnie, np