PB032276

140

DEFINK

I Ciąg¹^ 5i ** 52* 5₃*

S„*

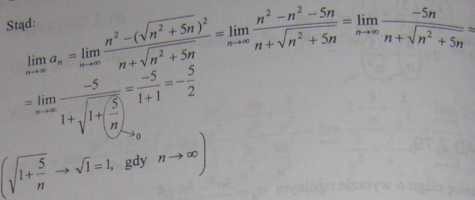
nazyw

szereg

+ a

,2. szereg geometryczny

1    1    1 ^ _J[_

ciągu: fl|⁼ 1> ^a2 ⁼2’°³    4’ ⁴    8

myci,g(Wi<«»^{suracIfici0WyCh:}

q=\. Wypiszmy koleją

• ’^a" ⁼(i) ’-'^anasiwt^

Jeżeli ci metryc:

my:

5 =

A

Wyra fli + a

,1 ,1

5'₂ = fli+fl2 = ^{1 +} 2⁼ 2

1 1 B*

Ą = a\ + a₂ + a% = 1+ « ⁺7 ”¹

£4 = a\ + a₂ + 03

2 4    4

1    1    1,7

⁺ fl4 = 1+2 ⁺ ^⁺8 8

1 1 1

15

5’₅ = _ai+ez₂ + a3 + a₄ + a₅ = H--+- + _i + —-H₁₆

Jeżeli s tej sum

TWIEF Jeżel jest z

S_n = a\ + + a-i +... + a_n =

1    1    ¹

1+-+-2 4

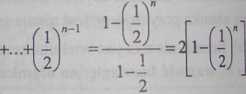
Dowód

Poniev

Można zauważyć, że jeśli ilość składników sumy S_n wzrasta nieograniczenie, to tasianis się coraz mniej od pewnej liczby, a mianowicie od 2.

To spostrzeżenie można potwierdzić rachunkiem:

lim

n-+co

lim S„ = lim 2-

ii’		mm
IB	= lim 2- lim
L W _	n—*to n—>co	UJ
		-^0

21 = 2.

rzy obliczaniu granicy wykorzystaliśmy twierdzenia dotyczące działań na

(<h - vw A zater

5 =

wzór: