PID1

-A-

Cyfrowy regulator ciągły PID

Algorytmy regulacji stosowane w regulatorach

Algorytm PID

Algorytm PID był praktycznie jedynym algorytmem regulacji w regulatorach analogowych i jest obecnie jeszcze nadal podstawowym algorytmem we wszystkich cyfrowych urządzeniach regulacyjnych.

W dziedzinie czasu algorytm ten można zapisać w następujący sposób:

y(0 = K_P

yc

^c(0 ⁺ Je(t)dt ^{+ Tr}

a odpowiednia zależność operatorowa przedstawia się następująco:

1

Gr(s) = ^^ = K_p ^R Ae(s) ^P

1 +-+ sTd

^sTC

Realizacja działania P, I oraz D

W rozdziale 3 przedstawiono czasowe i operatorowe funkcje regulatora PID. Dla regulatora P zależności te przedstawiają się w sposób następujący:

y(0 =    + y₀

^GrM = ~ = K_p

Ae(s)

Dla regulatora PD

yo

y(t) = Kp| e(t) + T_r ~^“j ⁺

^{Gr (s) =}    = Kp[l + ^sTr ]

Dla regulatora PI

y(t) = K,

^c(0 + rr/e(t)dt

y_c

1

sT_C

°R(^S) = ^-Kp

Ae(s)

Z powyższych zależności widać, że w regulatorach P oraz PD występuje stały sygnał podporowy y₀. Potrzeba istnienia tego sygnału wynika z następującego rozumowania. Przy jego braku i przy sygnale uchybu regulacji równym zeru sygnał wyjściowy regulatora byłby także równy zeru. A przecież sygnał wyjściowy powinien się zmieniać także przy ujemnych wartościach uchybu regulacji. Stąd przy zerowej wartości uchybu regulacji powinna istnieć niezerowa wartość sygnału wyjściowego regulatora określana właśnie stałym sygnałem podporowym y₀. Przykładowe charakterystyki statyczne regulatorów P oraz PD przedstawione są na rys. 4.1. Mają one wspólny punkt przecięcia dla e=0. Wartość stałego sygnału podporowego y₀ jest odpowiednio dobierana dla konkretnego układu regulacji. Za pomocą tej wartości następuje dopasowanie do punktu pracy i zakresu pracy urządzenia pomiarowego i urządzenia wykonawczego.    _

y - sygnał wyjściowy regulatora, e - uchyb regulacji, t - czas,

Kp- wzmocnienie regulatora,

T_c - czas całkowania (zdwojenia) regulatora,

T_R - czas różniczkowania (wyprzedzenia) regulatora, y_c - warunek początkowy całkowania,

G_r(s) - transmitancja regulatora, s - operator Laplace’a.

Wzmocnienie regulatora K_P wynika z nachylenia charakterystyki statycznej regulatora P (lub PD) y = f(e). Można je także określić na podstawie przebiegu sygnału wyjściowego regulatora P otrzymanego po skokowej zmianie uchybu regulacji przedstawionej na rys. 3.1. Wtedy wzmocnienie regulatora wynosi

e	Kr =—. óe
		AC
>	^1
		Ay
Rys. 3.1. Odpowiedź cz Czas całkowania regu uchybu regulacji przedst< którym działanie całkuje skokowej zmianie uchybu e	t asowa regulatora P na skokową w czasie zmianę uchybu regulacji atora wynika z odpowiedzi regulatora PI na skokową zmianę iwionej na rys. 3.2. Czas całkowania jest to więc czas, po ice regulatora jest równe działaniu proporcjonalnemu po regulacji.

i

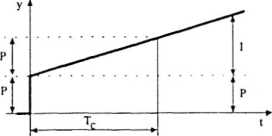
Rys. 3.2. Odpowiedź czasowa regulatora PI na skokową w czasie zmianę uchybu regulacji