skanowanie4 (3)

1.27.    a) Tenacoctr z pokoje, w którym wskazywał 20*C. no zewnątrz, gdzie panował 5*C chłód Po jednej nmnrio no tsrmcoecrse było jui 12*C. Po jakim cum termometr będzie wskazywał temperaturą tylko o 10 % wyższą aa khytm?

b) Golo, którego temperatura wynosi 22CC umieszcaooo w pomieszczeniu o temperaturze 0O*C. Po 10 minutach jego temperatura obniżyła się do 140*C. W tym momencie włączono klimatyzatory, które obniżają temperaturę otoczenia o szybkością 1*C na minutę. Jako będzie temperatura 7 dało po I minutach od chwili uruchomiania

Uhnasyzatorów?

1.28.    a) W obwodzie iśakrrycTnym pdągcoo aieragowo opornic o oporności R = 10 [O]. cewkę o indukcyjncóci L - 2 W oraz źródło oapśędo stałego £(0 « M M- Wyznaczyć graniczne natężenie prądu w obwodzie, gdy t - eo. Kaaakkowoć funkcję /(I) JA). jeM /(O) » 0 2 (A).

b) W obwodzie ałektiycsnym połącnooo wagowo opornik o opon* i? - 5(0], cewkę ₀ indukcyjności L» 2 5 H] oraz zewnętrzną silą ełektrocnoweyczną £(1) » 10 siu t (Vj. Wyznaczyć natężenie prądu /(i) [A] w obwodzie, je*ar/(0)-0.

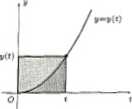
1.29.    Krzywo y - |(d przechodzi przez początek układu współrzędnych I leży w górną) półplaszczyźnie. Każdy prostokąt ograniczony odami układu współrzędnych i proftymi poprowadzonymi z dowolnego punktu (t.y(f)) krzywą) prostopadłymi do nieb krzywa y(t) dziali na dwie częśd Pole zawarte pod krzywą y(f) jest dwa razy wmtoj—» niż pole nad krzywą- Wyznaczyć równanie tą) krzywej

Lista piąta_____

1.50. Wyznaczyć rozwiązania podanych równana*) rządu drugiego:

■)*V-(l0^ł-0s    e) - (jO*-1; d) y"e« 2^ ♦ śf⁵

1J1. Rozwiązać (ecalkować) podane równania różniczkowo:

■)lV+l«0!    b)2yy'-3(y')*-4y*; c) (y-1)^-2<✓)*;    d*)

1.32.    Rozwiązać podane równania różniczkowe z zadanymi warunkami początkowymi:

a)    P*'=7+p. f(2)-0.r'(2)-4; b) **-&')*»✓ In V. y<0) - 1. ^(0) - 1;

«) V - V. y<-a) -1. ✓(-« - is d) ty* _s tfl+rO. y(i) - o. ✓<!) - -L

1.33.    Znaleźć krzywą y w y(t), która prsedłodzl przez punkt (0.1) i jam w nim etyczna do prostej t + y ■ 1 oraz spełnia równanie różniczkowe yy* + (yT ^— 1.

1.34.    a) Wyznaczyć równanie ruchu spadającego swobodnie dala o mazie m t uwzględnianiem oporo powwcna. który jost wprost proporcjonalny do kwadratu prędkoid spadania, ze współczynnikiem proporcjonalności k > 0 Przyjąć, że dało spada t wysokość Jt przy zerowej prędkości początkowej.

b)    Crąstcrrka o masie m porusza się po licE prostej. Niech r(t) oznacza odległość tej cząsteczki w chwil t od wtalowsgc azwn aa promsj W’ punhde x crąstecria jest przyciągana ptmz centrom » ślą kr**. gdde k > 0. Wyznaczyć równanie niebu cząsteczki oraz znaleźć jego rozwiązanie, jeżeli rozpoczęła ona rock w odległości ją od centrum z zerową prędkością początkową. Obliczyć czas. po którym cząsteczki osiągnie centrum

4