14887 skanuj0001,6
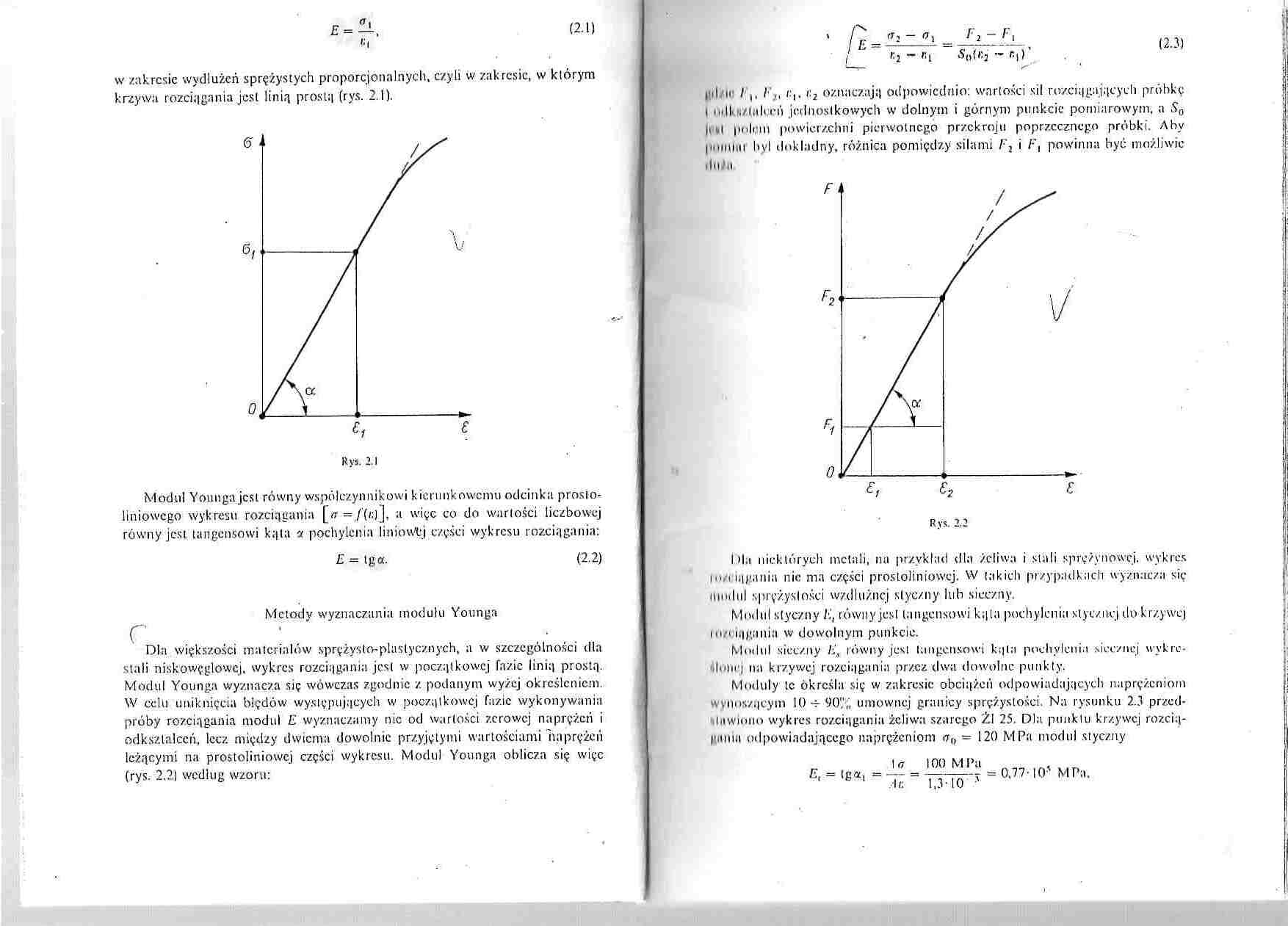
(2.1)
w zakresie wydłużeń sprężystych proporcjonalnych, czyli w zakresie, w którym krzywa rozciągania jest linią prostą (rys. 2.1).
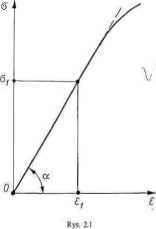
Modni Younga jest równy współczynnikowi kierunkowemu odcinka prostoliniowego wykresu rozciągania [u ■/(*)], a więc co do wartości liczbowej równy jest tangensowi kąta i pochylenia liniowej części wykresu rozciągania: £ - Iga. (2.2)
Metody wyznaczania modułu Younga
c
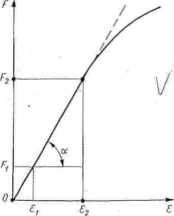
Dla większości materiałów sprężysto-plastycz.nych, a w szczególności dla stali niskowęglowcj. wykres rozciągania jest w początkowej fazie linią prostą. Moduł Younga wyznacza się wówczas zgodnie z podanym wyżej określeniem. W celu uniknięcia błędów występujących w początkowej fazie wykonywania próby rozciągania moduł £ wyznaczamy nic od wartości zerowej naprężeń i odkształceń, lecz między dwiema dowolnie przyjętymi wartościami naprężeń leżącymi na prostoliniowej części wykresu. Moduł Younga oblicza się więc (rys. 2.2) według wzoru: (2.3)
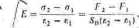
l|il/n' I |, r, oznaczają odpowiednio: wnrlości sil rozciągających próhkę
i iii|ks/litlecń jednostkowych w dolnym i górnym punkcie pomiarowym, a S0 |i tl polem powierzchni pierwotnego przekroju poprzecznego próbki. Aby IiMinliii byt dokładny, różnica pomiędzy silami F, i F, powinna być możliwie duła
F
l ila niektórych metali, na przykład dla żeliwa i stali sprężynowej, wykres io/i iiijiania nic ma części prostoliniowej. W takich przypadkach wyznacza się (iiinlul sprężystości wzdłużnej styczny luh sieczny.
Moduł styczny K, równy jest tangensowi kipa pochylcnist stycznej do krzywej m/t ii|gtinia w dowolnym punkcie.
Modni -sieczny li, równy jest tangensowi kipa pochylenia .siecznej wykre-4|»nqj tlił krzywej rozciągania przez dwa dowolne punkty.
Moduły te określa się w zakresie obciążeń odpowiadających naprężeniom wynoszącym 10+ W,, umownej granicy sprężystości. Na rysunku 2.3 przed-diiwiniio wykres rozciągania żeliwa szarego Żl 25. Dla punktu krzywej rozciąganiu odpowiadającego naprężeniom o„ = 120 MPa moduł styczny
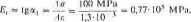
Wyszukiwarka
Podobne podstrony:
skanuj0003 (324) E =li(2.1) w zakresie wydłużeń sprężystych proporcjonalnych, czyli w zakresie, w kt
skanuj0030 3 W zakresie sprężystym wpływ /brojenia dodatkowego przy otworach st wyrażony wzorami Fme
skanuj0250 (4) • zakres regulacji prędkości obrotowych, niezbędnych w maszynach roboczych, jest najc
skanuj0250 (4) • zakres regulacji prędkości obrotowych, niezbędnych w maszynach roboczych, jest najc
skanuj0001 3 ZAKRES MATERIAŁU NA KOLOKWIUM NR I 1. Scharakteryzuj podziały aminokw
skanuj0015 5 Zakres tematyczny: OGÓLNA TECHNIKA BUDOWLANA W tym rozdziale omówione są następujące
skanuj0055 3 Zakres tematyczny: MURARSTWO W tym rozdziale omówione są następujące tematy: Rodzaje
(wielkość sorpcji jest proporcjonalna do wydłużenia sprężyn). Na podstawie otrzymanych wyników
38164 skanuj0086(1) Zakreśl w kolorowe pętelki pary takich samych liter, według wzoru.
27390 skanuj0265 (4) Zarys ewolwentowy. Ewolwentą (rozwiniętą) koła nazywa się krzywą, którą zakreśl
więcej podobnych podstron