28518 skanuj0058 (50)

72 Mathcad. Ćwiczenia

Wykres przestrzenny powierzchni parametrycznej

Program otrzymuje wektorową funkcję dwóch parametrów. Uzyskany wynik jest traktowany jako wektor wodzący powierzchni rozpiętej w przestrzeni trójwymiarowej. Oczywiście końcowa postać uzyskanej powierzchni silnie zależy od wybranego układu współrzędnych.

Ćwiczenie 5.3.—*&<$*•-

Wykreśl powierzchnię torusa zdefiniowanego równaniami parametrycznymi: x = (1 + cos u) cos v s y = (1 + cos u) sin v , z ⁼ sin u

gdzie parametry u i v mają przedziały zmienności od 0 do 2n.

1. Zdefiniuj wektorową funkcję dwóch argumentów zgodnie z powyższymi równaniami (rysunek 5.17).

Rysunek 5.17.

Wektorowa definicja równań torusa

G(u,v)

(2 + cos(u))cos(v) (2 + cos(u))sin(v) sin(u)

2. Wywołaj szablon Surface Plot trójwymiarowego wykresu kartezjańskiego, np. wybierając menu rozwijane Insert, podmenu Graph, polecenie Surface Plot. Do pola w lewym dolnym narożu szablonu wpisz nazwę funkcji i naciśnij klawisz Enter.

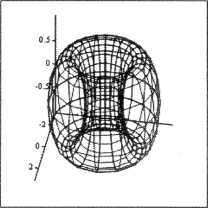
Na ekranie pojawi się powierzchnia torusa (rysunek 5.18).

o

Rysunek 5.18.

Powierzchnia torusa

3. Jak widać na rysunku 5.18, torus jest zniekształcony, gdyż skala osi pionowej jest inna niż osi poziomych. Należy też pamiętać, że Mathcad przez domniemanie przyjmuje przedziały zmienności parametrów od -5 do 5 z krokiem 0.5. W rozważanym tu przypadku należy ustalić przedział zmienności od 0 do 27t, dobierając krok podziału tak, aby modelowana powierzchnia była w miarę gładka. W tym celu nasuń kursor myszy na wykres i jeden raz kliknij lewym klawiszem myszy, aby zaznaczyć wykres.