29369 SDC14203

Rysunek 6

Przegląd mierników stMtyatycznych

M.ary

dywersji

WW*fn*i ifruMiwy

VW»kfl*1iW

niecna

ŚłBOn lo

ydruncia

pozycyjne

Tkmpo

wzrostu

Li Arytmetyczna		Mediana
f—ś Geometryczna		Dommanta
4 Warmnnczna		Kwaityte
L4 Kwadratowa

zaobserwowane wartości zmiennej w całej badanej zbiorowości i podzielić przez liczbę jednostek tej zbiorowości. Wśród miar przeciętnych najpopularniejsza jest dominanta (inaczej wartość nwdalna), która oznacza wartość najczęściej | spotykaną, najbardziej typową.

Innymi miarami pozycyjnymi są kw ar tyle, z których najczęściej używany jest kwarty! drugi, czyli mediana (inaczej wartość środkowa).

Mediana rozdziela całą zbiorowość na dwie liczebnie równe części w ten sposób, że w jednej z nich znajdują się jednostki o wartościach niższych od mediany, a w drugiej — o wartościach wyższych od mediany.

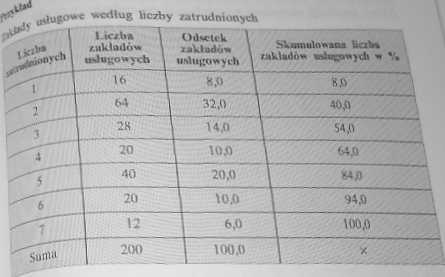
Przeciętną liczbę zatrudnionych w zakładzie usługowym otrzymujemy przez podzielenie liczby ogółu zatrudnionych pnez liczbę zakładów usługowych:

1 16-

2-64 + 3-28 +4-20 + 5-40+6-20+7-12 721

2ÓT    -2M"^3,56,

co oznacza, że przeciętnie w jednym zakładać usługowym utrudnionych jest 3,56 osób. Dominanta (wartość najczęściej występująca) wynosi 2 zatrudnionych, natomiast mediana - 3 zatrudnionych, co oznacza, że w połowie zakładów zatrudnionych jest mniej niż 3 pracowników.

Gdy rozkład danej cechy jest symetryczny, wtedy średnia arytmetyczna, mediana i dominanta są sobie równe. Natomiast gdy rozkład nie jest symetryczny (przesunięty w prawo lub lewo), każda z wartości jest inna (rysunek 7).

W wypadku badania dochodów wartość średnia jest na ogół większa od mediany. Średnia arytmetyczna jest bowiem zawyżona przez dochody osób najbogatszych, podczas gdy