42019 skrypt2

(5 44)

(5.45)

(5 46) -

(5.47)

(5.48)

(5.49)

Przedmiot niniejszego rozdziału stanowi zagadnienie piaktycznej realizacji algorytmów cyfrowej filtracji ortogonalnej sygnałów losowych drugiego rzędu

Dotychczasowe rozważania dotyczące zagadnień prognozy, filtracji innowacyjnej modelowania stochastycznego oraz. filtracji odszumiającej, były oparte na założeniu, iż punktem wyjścia jest zbiór wartości obserwowanego (na skończonym odcinku czasu {t.r- !,...,/-«}) stacjonarnego (w szerszym sensie) sygnału losowego drugiego rzędu, o czasie dyskretnym Innymi słowy, przyjmowaliśmy dotąd założenie, że znany jest zbiór zmiennych losowych {y(fj, y(f — l),...,y(f — n)} sygnału obserwowanego Podejście takie było niewątpliwie naturalne i wygodne przy formułowaniu oraz przy rozwiązaniu (lak algebraicznym, jak i geometrycznym) wymienionych zagadnień cyfrowej filtracji ortogonalnej, umożliwiając m in. zwartość zapisu przy wyrażaniu (pizy użyciu operatora uśredniania probabilistycznego E) rozważanych statystyk sygnałów, jak również klarowną interpretację zmiennych losowych (jako elementów przestrzeni Hilberta) w podejściu geometrycznym.

W praktyce najczęściej dysponujemy skończonym naborem próbek ( vo,vt, ■. yr} jednej realizacji sygnału losowego, obserwowanej na skończonym odcinku czasu {0,1,.. ..T} (gdzie0jest umownym „początkiem"obserwacji, a chwila T -jego „końcem"). Wówczas - przyjmując hipotezę ergodyczną (na mocy którei w obserwowanej realizacji z prawdopodobieństwem równym I odzwierciedlają się wszystkie właściwości statystyczne rozważanego sygnału losowego) - wymagane statystyki sygnału uzyskuje się na drodze uśrednienia w czasie obserwowanej realizacji, wielkościami zaś transmitowanymi w strukturach filtrów są

6.1.

5.3.

Liniowa cyfrowa filtracja ooszumiaj/jca sygnałów Zatem

= (*n( '),<('))« =

= MO - Ip,M(0M0 - X>M(0)« =

1=0    /-o

= MO.40)«- Zp,^r‘M0.n(0)t/ +

r—o

~ ZP'(^r<(OMO)u+ X Ż P’Pl(^r‘(<).rdt))v -

teO    /=01=0

= IMOII^,-2ilpfl^ł + tl«'l² =

/=0 <=0

= IMOII²-XlPO^J

t=0

Zauważmy, źc jeśli R'_n -y O gdy w —> oo to otrzymujemy równość Parsevala

IWO Ili = £ip/'l²

i-0

Zauważmy również, żc z (5.28) otrzymujemy P(53)4/) = P(^-') + P(r„(r)).x(0 a stąd

i„(0=.?n-l(0+P_n^V"(0

Żalem

<(0=40-^-i(0-pM40 = <-i(0 - PiJMO

i w konsekwencji

= «(0.<(0)u =

= «-l (0 - P?r,(0,«J- I (0 - Pn^r"(0)tl =

= «-i(0.*»-ifO)t/-pJ«-i(0.^(0)u-p^''»(0-<-i(0)u +

+lpil²M0i^r»(O)« =

= /?!-■-|p„f

128

6. Cyfrowa filtracja adaptacyjna szeregów czasowych

_____OmOGOMALHA REALIZACJA OPTYMALNEGO FILTRU OOSZUMlAJAe.Enn

Ortogonalna realizacja optymalnego filtru odszumiającego

Z rozważań przeprowadzonych w poprzednim podrozdziale wynika. Ze w celu otrzymania estymatorami) jest wymagana znajomość bazy ON (r_j(r))]’ „pod-przestrzeni obserwacji SJJ.

Zauważając (np na rys 3.10), Ze błędy prognozy w tyl. wyznaczane w dolnej gałęzi filtru prognozującego (innowacyjnego) stanowią wiośnie elementy poszukiwanej bazy ON (zgodnie z (5.30)). filtr innowacyjny moZemy w obecnie rozważanym kontekście zinterpretować jako "generator" bazy ON podprze-strzem ,5'fJ Obserwacja ta. wraz z zależnościami (3.3). (4 40). (4.41). (5.41) oraz

(5 47) implikuje pomZszy algorytm optymalnej ortogonalnej filtracji odszumia-

jącej dla n = 1,. ..p:

Kroki:    p„ =    F>„_ i(r)r„„ i(f - 1)    (5.50)

Krok 2:    e„(f) = (I    - p„²)'ł[e„-i(f) + p„r._,(f    - 1)1    (5.51)

Krok 3:    r„(r) = (I    - p2)‘Hp«^e"-i(0 + ^r"-t('    ~ 01    <5.52)

Krok 4:    p„' =-. c_yr(0)B„.„ 4 . I- c„(n)B„,o    (5.53)

Krok 5:    .?„_,((} =    f„-z(0 + pi-i^-it')    <^{5 54}1

Inicjalizacja:    en(t) = ^ro(0 = y(0 • ^-l(0 ⁼ 0

Algorytm ten implikuje ortogonalną realizację optymalnego filtru odszumiającego. przedstawioną na rys 5.6

RYS. 5 6

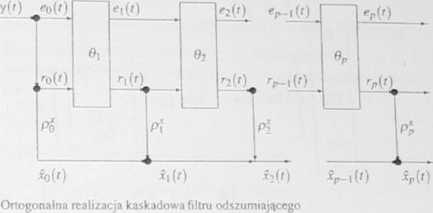
1111

Notacja

próbki omawianej realizacji sygnału losowego. Mówi się wówczas o cyfrowej filtracji szeregów czasowych.

Celem niniejszego rozdziału jest prezentacja algorytmów cyfrowej filtracji ortogonalnej szeregów czasowych W rozdziale tym zostanie pokazane, że jeśli punktem wyjścia do rozważań omawianej wcześniej klasy algorytmów cyfrowej ortogonalne) filtracji średniokwadratowejjest nabór próbek pojedynczej realizacji sygnału obserwowanego, to „optycznie" wystarczy zastąpić zmienne losowe próbkami sygnałów we wszystkich dotychczas przedstawionych algorytmach i ich realizacjach za pomocą grafów przepływowych Jedyną różnicę stanowi metoda estymacji parametrów filtrów, oparta na uśrednianiu czasowym naboru próbek W celu zbliżenia się do realizacji omawianych filtrów w czasie rzeczywistym zostaną przedstawione metody uaktualniania w czasie parametrów filtrów, prowadzące do algorytmów cyfrowej ortogonalnej filtracji adaptacyjnej szeregów czasowych [35]

Niezależnie od modularnej struktury tych algorytmów, ich samorzutnej stabilności numerycznej i odporności, malej wrażliwości na błędy zaokrągleń, charakteryzują się one znakomitymi właściwościami w odniesieniu do zbieżności oraz bardzo szybkiego śledzenia zmian parametrów filtrów. Wynika to z faktu, iż prezentowane dalej algorytmy stanowią „dokładne" rozwiązanie problemów filtracji średniokwadratowej dla każdego naboru próbek (tj„ dla każdego T = 0,1,2.....gdzie T można interpretować jako czas bieżący). Dlatego

też prezentowana klasa algorytmów nadaje się bezpośrednio do implementacji (również wieloprocesorowej) i umożliwia realizację cyfrowych ortogonalnych filtrów optymalnych w czasie rzeczywistym.

Notacja

Niech będzie dany, zbiór próbek (yo____,yr}. gdziey, 6 %. W niniejszym roz

dziale będziemy wykorzystywać tzw. notację brackelową [35J. W tym celu wprowadźmy wektor typu ..ker" jako

\y>r=[ya - yr]'    <^6I>

gdzie ¹ oznacza transpozycję. Zatem |y >t jest wektorem ko/umnowym próbek, który możemy interpretować jako element przestrzeni wektorowej

’H = x ... x !Ą_. Określmy wektor typu „bra" ja ko

r+i

130

131