44911 image001 (35)

Wulital InformatyM Wtl

Egzamin z matematyki dyskretnej (D)

§jRl^:S ■    .....

UWAOAI W trakcie rozwiązywania zadań nalaży krótko objaftntat postępowania powołując s»* na twierdzenia lub zagadnienia kombinałoryczna, t których »ią korzysta

Wyhlkl obliczeń itanowiąca rozwiązania zadań nalany wyróżniać poprzedzając je skrótem „Odp

Nie mogą ona zawierać aymboll potęgi ubywającej i przyrastającej, silni oraz współczynnika dwumianowego i wielomianowego; mogą być przedstawiona w postaci wyrażeń arytmetycznych zawierających symbołe operacji dodawania, odejmowania mnożenia i dzielenia ora# zwykłego potęgowania

należy wyznaczać rekurencyjnie

Potrzebne wart olei liczbowe Pih_t k) i

lp.

Aodftnit

Maks, pkL I l/zysk. I

V1nmy do dyspozycji 9 osób, wśród których są dwie grupy narodowościowe: ojc Węgrów i czworo Finów.

ile sposobów można ustawić tc 9 osób w szereg tak. żeby osoby żadnej / ty ch dwóch narodowości nic stuły w komplecie obok siebie?

... _______ _ A
	,—1—		JM	J
	ci		\ 1	W\
i—_	7	’ 1 11
		i°t
		iiT:

n

Ile jest na podanej kracie ulic najkrótszych dróg /. A do B. które przechodzą przynajmniej przez jedno z zaznaczonych skr/N zowań C, D lub E?

Ile jest nicujcmnych i całkow itych rozwiązań nierówności .tj ⁴ *2 '^f *3 ⁴ x4 ⁴ *5 ⁴ xh £'9*

które spełniają warunki

(L

1 .V-. +■ X-

Xa + X,

lic różnych ciągów sy mboli zawierających 4 niepowtarzające się litery i 5 cyfr można utworzyć w ybierając litery ze zbioru (a, b. c, d, e. f. g. h. i i oraz cyfry ze zbioru {J. 2,3,4,5.6,7}?

Na ile sposobów można rozdzielić 13 jednakowych procesów pomiędzy 4 jednakowe procesory tak. aby na jednym z nich zostały wykonane dokładnie 4 procesy?

Rozdzielić trzeba wszystkie procesy, żaden z procesorów nie może pozostać bezczynny i każdy proces musi być w całości wykonany na jednym procesorze.

6.

7.

Narysuj wszystkie nieizomorficznc ze sobą grafy o $ wierzchołkach i 5 krawędziach.

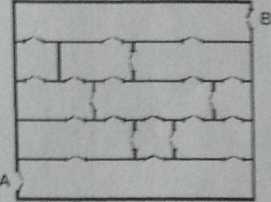
Rozstrzygnij z uzasadnieniem w oparciu o teorię grafów, czy można zwiedzić piętro budynku o podanym obok planie tak. aby wejść drzwiami A. wyjść drzwiami B i przejść przez każde z zaznaczonych drzwi dokładnie raz.

Narysuj Rrtrfreprezentujący zadanie i opisz rozwiązywane łagodnienie w języku teorii grafów.

3

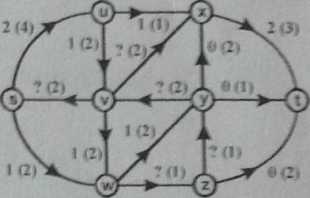
W podanej sieci (przy łukach podano wartości przepływów i w nawiasach ich przepustowości) wyznacz:

brakujące wartości przepływów przez łuki (ozn. ?) tak. że zostanie zdefiniowany przepływ przez tę sieć; wartość maksymalnego przepływu z s do t za pomocą kolejnych ścieżek powiększających przepływ: minimalny przekrój pomiędzy s i t oraz jego przepustowość (zilustruj tw. Forda i Fulkersona).

Podróżnik odwiedzi! pewien daleki kraj 1 zapisał w swojej relacji z podróży: „W tym pięknym kraju jest 8 dużych miast. Wiele z nich połączonych jest ze sobą utwardzonymi traktami, które nigdzie poza miastami się nic krzyżują. W każdym mieście początek traktu wskazuje specjalna brama z nazwą miasta, do którego on prowadzi Trzy najważniejsze miasta mają po 6 takich bram. W każdym z pozostałych są 4 takie bramy.'" /weryfikuj w oparciu o teorię grafów wiarygodność lej relacji.

a)

b) e)

r\

//

W pewnym grafie o 15 wierzchołkach maksymalna moc skojarzenia wynosi 7. lic wynosi minimalna moc pokrycia krawędziowego w tym grafie?

Czy może w nim istnieć wewnętrznie stabilny zbiór wierzchołków o mocy 9? Odpowiedzi dokładnie uzasadniaj.

/

1 n» lit oe 43 ą.

SUMA:

50

<r>

jf

c.

m

10.