49556 Untitled Scanned 35 (6)

można we wzorze (13.29) wielkości stale wynieść przed znaki całek i po scałkowaniu pozostałych — otrzymać:

(13.32)

gdzie: co, — pole wykresu momentów od X, = i.

Przed pierwszym wyrazem stawiamy znak plus, gdy nierównomierny przyrost temperatury At powoduje wydłużenie tych samych włókien pręta, które również są rozciągane pod wpływem obciążenia X, = l. W przypadku przeciwnym, tzn. gdy jedno działanie powoduje wydłużenie, a drugie skrócenie tych samych włókien stawiamy znak minus.

Przed drugim wyrazem stawiamy wówczas znak minus, gdy siła X,= 1 powoduje skrócenie, a temperatura wydłużenie osi pręta lub odwrotnie. Znak plus postawimy wtedy, gdy efekty obydwu wpływów będą jednakowe.

Wyrażenie (13.32) określa przemieszczenie układu podstawowego na kierunku działania siły X, powodowane zmianami temperatury.

13.7.2. Siły wewnętrzne powodowane zmianami temperatury

Po wyznaczeniu wartości przemieszczeń A_it od zmian temperatury możemy przejść do obliczenia sił w układzie statycznie niewyznaczalnym, wywołanych tymi zmianami.

Rozwiązując równania kanoniczne określamy wartości (od wpływu zmian temperatury) nadliczbowych niewiadomych, a na ich podstawie obliczamy siły wewnętrzne M, T i N.

Przebieg postępowania przy obliczaniu sił wewnętrznych wywoływanych obciążeniem termicznym pokażemy na przykładzie.

Przykład 13.4. Wyznaczyć wartości sił wewnętrznych w ramie poddanej wpływom zmian temperatury (rys. 13.38a).

Układ podstawowy przyjmujemy jak na rys. 13.38b. Obliczamy następnie:

td + te ~2

40-20

~2

= 10°C tzn. 10 deg;

At=td — t„ = 40 + 20= 60°C tzn. 60 deg.

W rozpatrywanym przykładzie powyższe wielkości są takie same dla obydwu prętów. Równanie sumy ■rcreinieszczeń na kierunku X, przybiera postać:

<5n Xi + złi,=0.

Do określenia wartości <5_tl potrzebny będzie wykres momentów od jednostkowej wartości nadżerkowej siły X_l — 1, a do określenia A_u ze wzoru (13.32) także wykres sił podłużnych od X, = l. Wykres Mi pokazano na rys. 13.38c, a A/, — na rys. 13.38d. Obliczamy wartości S,, i A_u:

11    2    1

<5n =---15 -15 — -15 = 1125— ;

EJ 2    3    EJ

1 coAt \ A-15-15-60    \

Au=«l ±-j- ±Nlt\ = a. I -—--1 • 5• 101 = 6700a.

rozstawieniu obliczonych wartości do równania wyjściowego otrzymamy:

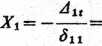
6700a EJ 1125

-5,95 aEJ.

473